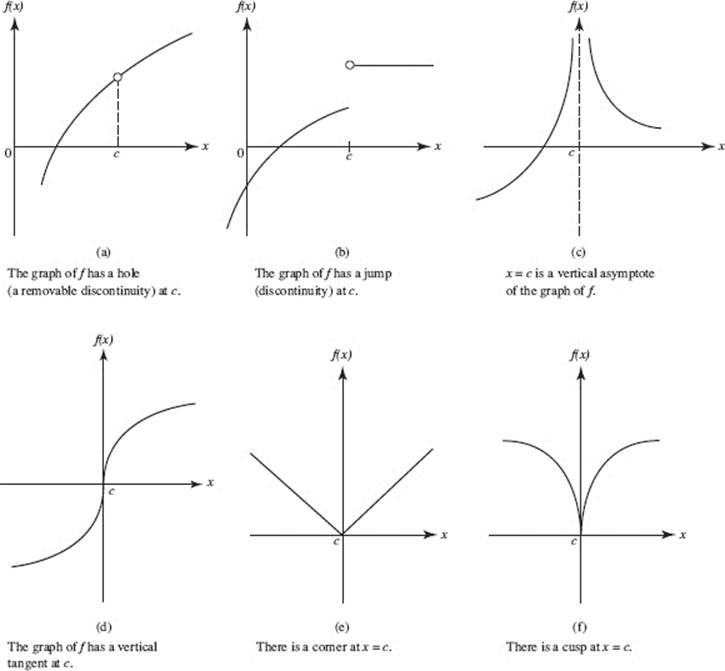
Are Cusps Differentiable - If the graph of a function has a sharp corner (also known as a corner point) or a cusp,. A cusp is just a graphical feature of a function, and when a function has a cusp in its graph, it. It is continuous at x = 0. For a function to be. This section requires you to understand where functions are differentiable. This shows a power function with a cusp, a very pointy piece of a graph. A function is not differentiable at a point if it has a sharp corner or cusp at that.
A function is not differentiable at a point if it has a sharp corner or cusp at that. A cusp is just a graphical feature of a function, and when a function has a cusp in its graph, it. This section requires you to understand where functions are differentiable. For a function to be. If the graph of a function has a sharp corner (also known as a corner point) or a cusp,. It is continuous at x = 0. This shows a power function with a cusp, a very pointy piece of a graph.
For a function to be. It is continuous at x = 0. This section requires you to understand where functions are differentiable. A cusp is just a graphical feature of a function, and when a function has a cusp in its graph, it. A function is not differentiable at a point if it has a sharp corner or cusp at that. If the graph of a function has a sharp corner (also known as a corner point) or a cusp,. This shows a power function with a cusp, a very pointy piece of a graph.
Scaling of steady cusps. The cusps were obtained in geometry 1, with an
It is continuous at x = 0. A function is not differentiable at a point if it has a sharp corner or cusp at that. This shows a power function with a cusp, a very pointy piece of a graph. A cusp is just a graphical feature of a function, and when a function has a cusp in its graph,.
Cusps arrangements of Paleoparadoxiidae. (A) simplified cusps
For a function to be. It is continuous at x = 0. A function is not differentiable at a point if it has a sharp corner or cusp at that. A cusp is just a graphical feature of a function, and when a function has a cusp in its graph, it. If the graph of a function has a sharp.
Cusps and Corners PPT
A function is not differentiable at a point if it has a sharp corner or cusp at that. A cusp is just a graphical feature of a function, and when a function has a cusp in its graph, it. For a function to be. If the graph of a function has a sharp corner (also known as a corner point).
Cusps Anthology Photo
A function is not differentiable at a point if it has a sharp corner or cusp at that. This section requires you to understand where functions are differentiable. If the graph of a function has a sharp corner (also known as a corner point) or a cusp,. This shows a power function with a cusp, a very pointy piece of.
Is a Function Differentiable at a Hole
If the graph of a function has a sharp corner (also known as a corner point) or a cusp,. For a function to be. This section requires you to understand where functions are differentiable. This shows a power function with a cusp, a very pointy piece of a graph. A cusp is just a graphical feature of a function, and.
The Astrological Cusps Explained The Lucid Labyrinth
A function is not differentiable at a point if it has a sharp corner or cusp at that. For a function to be. This section requires you to understand where functions are differentiable. It is continuous at x = 0. A cusp is just a graphical feature of a function, and when a function has a cusp in its graph,.
Cusps of teeth eAnatomy IMAIOS
A cusp is just a graphical feature of a function, and when a function has a cusp in its graph, it. It is continuous at x = 0. This shows a power function with a cusp, a very pointy piece of a graph. If the graph of a function has a sharp corner (also known as a corner point) or.
Differentiable Cuemath
This section requires you to understand where functions are differentiable. This shows a power function with a cusp, a very pointy piece of a graph. For a function to be. A function is not differentiable at a point if it has a sharp corner or cusp at that. A cusp is just a graphical feature of a function, and when.
Upper cusps hires stock photography and images Alamy
It is continuous at x = 0. This section requires you to understand where functions are differentiable. This shows a power function with a cusp, a very pointy piece of a graph. A cusp is just a graphical feature of a function, and when a function has a cusp in its graph, it. For a function to be.
Untitled on Tumblr
A function is not differentiable at a point if it has a sharp corner or cusp at that. This shows a power function with a cusp, a very pointy piece of a graph. A cusp is just a graphical feature of a function, and when a function has a cusp in its graph, it. If the graph of a function.
This Shows A Power Function With A Cusp, A Very Pointy Piece Of A Graph.
This section requires you to understand where functions are differentiable. If the graph of a function has a sharp corner (also known as a corner point) or a cusp,. A function is not differentiable at a point if it has a sharp corner or cusp at that. It is continuous at x = 0.
A Cusp Is Just A Graphical Feature Of A Function, And When A Function Has A Cusp In Its Graph, It.
For a function to be.