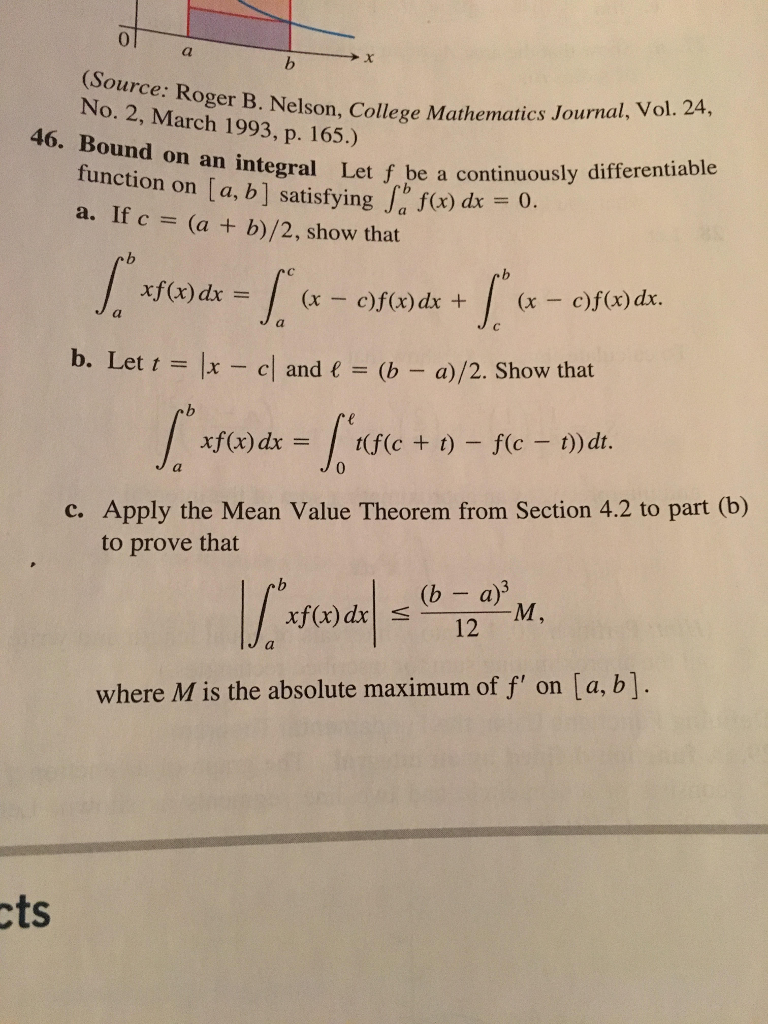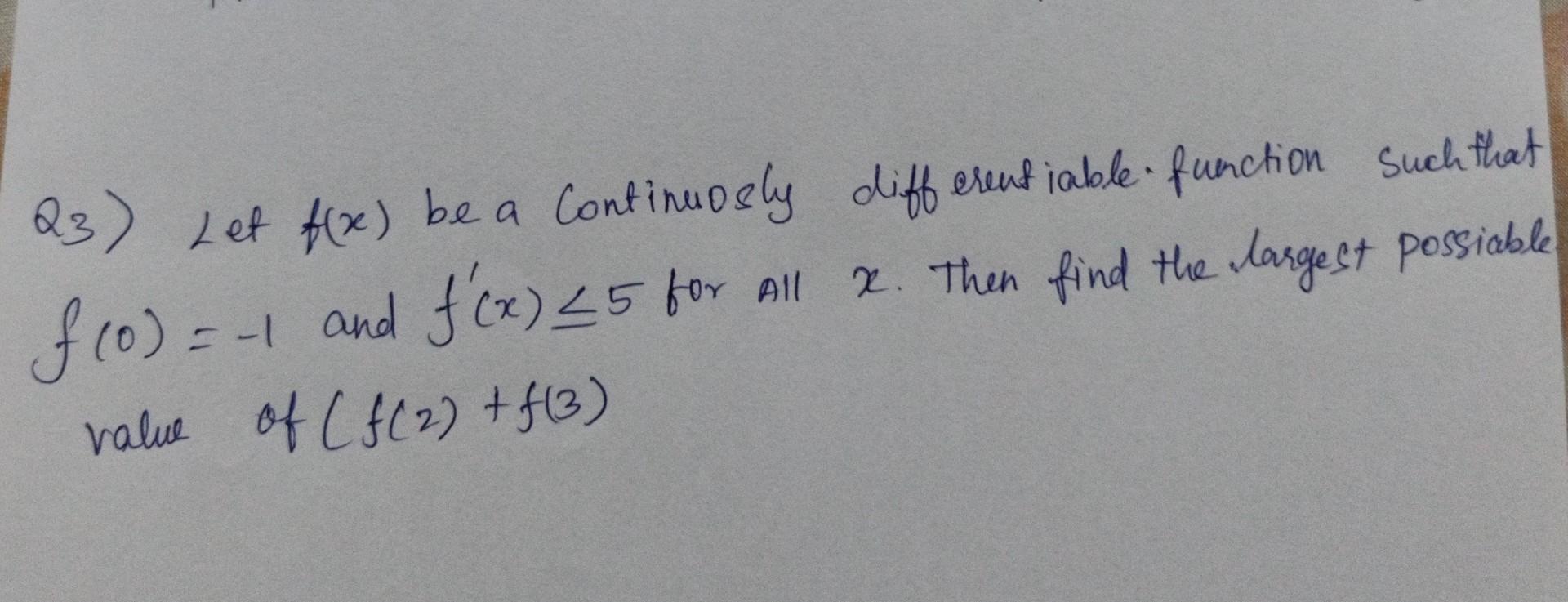Continuously Differentiable Function - A function is said to be continuously differentiable if its derivative is also a continuous function; A differentiable function $f$ is continuously differentiable if and only if $f$ is of. Simply put, differentiable means the derivative exists at every point in its domain. A continuously differentiable function $f(x)$ is a function whose derivative function. A function can be continuous at a point, but not be differentiable there.
A function is said to be continuously differentiable if its derivative is also a continuous function; A continuously differentiable function $f(x)$ is a function whose derivative function. A function can be continuous at a point, but not be differentiable there. A differentiable function $f$ is continuously differentiable if and only if $f$ is of. Simply put, differentiable means the derivative exists at every point in its domain.
A function can be continuous at a point, but not be differentiable there. A continuously differentiable function $f(x)$ is a function whose derivative function. Simply put, differentiable means the derivative exists at every point in its domain. A function is said to be continuously differentiable if its derivative is also a continuous function; A differentiable function $f$ is continuously differentiable if and only if $f$ is of.
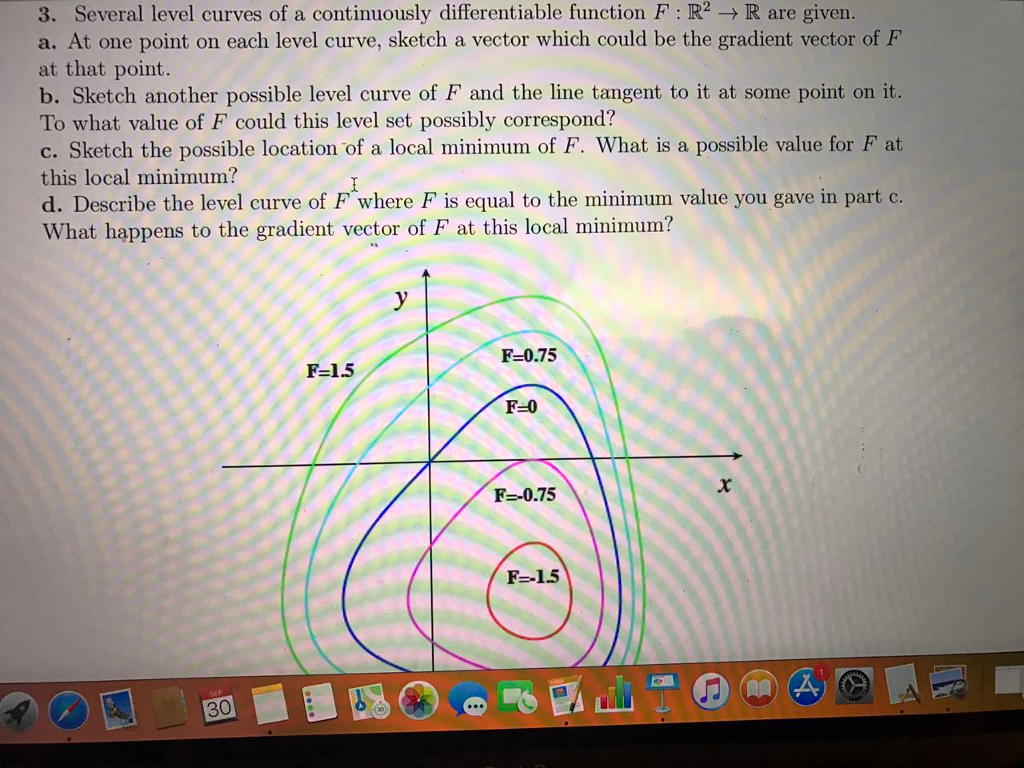
Solved 3. Several level curves of a continuously
A function is said to be continuously differentiable if its derivative is also a continuous function; A function can be continuous at a point, but not be differentiable there. A differentiable function $f$ is continuously differentiable if and only if $f$ is of. Simply put, differentiable means the derivative exists at every point in its domain. A continuously differentiable function.
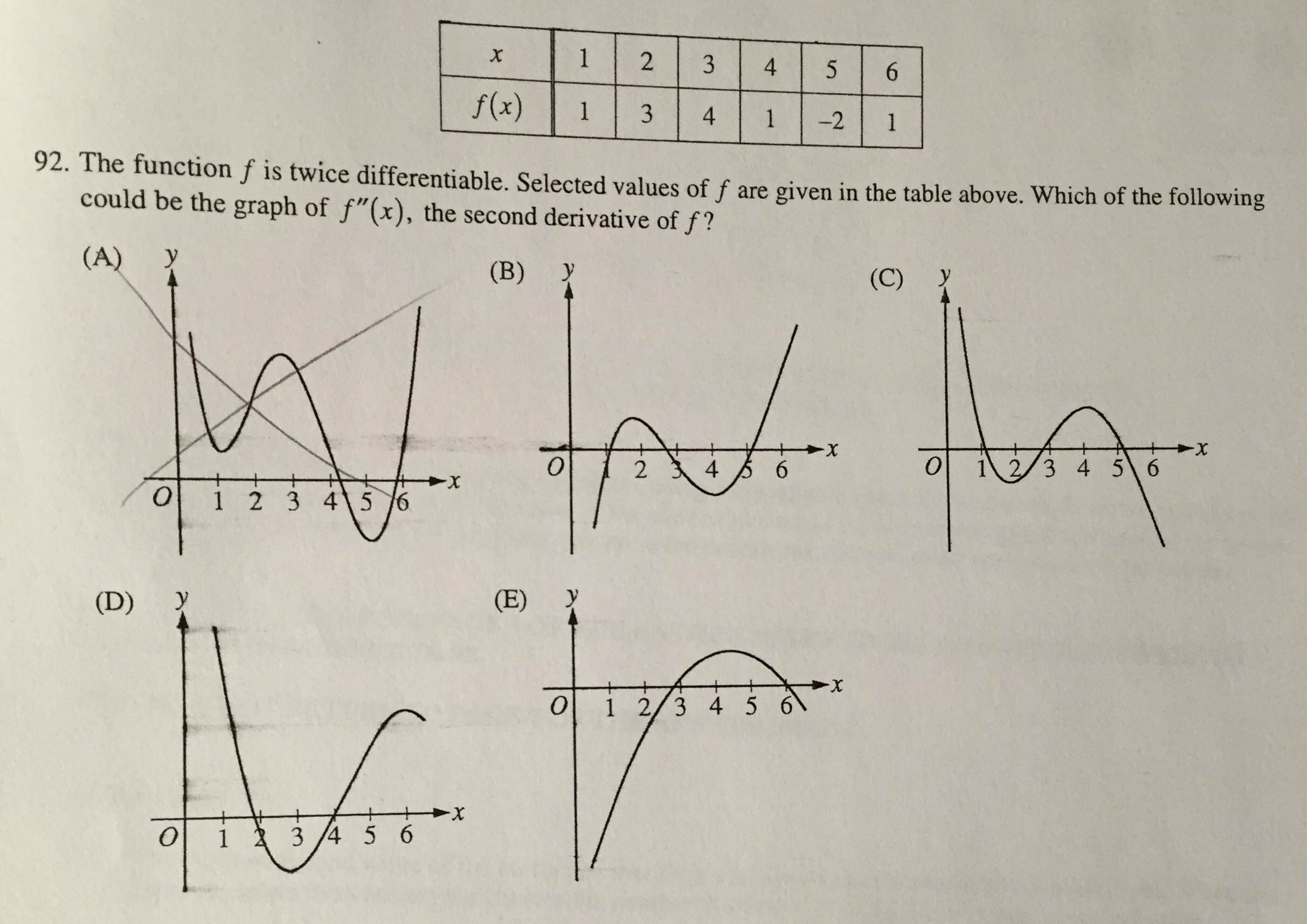
Twice Continuously Differentiable Function
A function can be continuous at a point, but not be differentiable there. A function is said to be continuously differentiable if its derivative is also a continuous function; Simply put, differentiable means the derivative exists at every point in its domain. A differentiable function $f$ is continuously differentiable if and only if $f$ is of. A continuously differentiable function.
Solved Problem 6 Given a continuously differentiable
A continuously differentiable function $f(x)$ is a function whose derivative function. A function is said to be continuously differentiable if its derivative is also a continuous function; A differentiable function $f$ is continuously differentiable if and only if $f$ is of. A function can be continuous at a point, but not be differentiable there. Simply put, differentiable means the derivative.
Solved Let f be a continuously differentiable function on
A function is said to be continuously differentiable if its derivative is also a continuous function; A continuously differentiable function $f(x)$ is a function whose derivative function. A function can be continuous at a point, but not be differentiable there. A differentiable function $f$ is continuously differentiable if and only if $f$ is of. Simply put, differentiable means the derivative.
5. Let f RnR be twice continuously differentiable
A function can be continuous at a point, but not be differentiable there. Simply put, differentiable means the derivative exists at every point in its domain. A function is said to be continuously differentiable if its derivative is also a continuous function; A differentiable function $f$ is continuously differentiable if and only if $f$ is of. A continuously differentiable function.
Solved Let f R + R be a continuously differentiable
A differentiable function $f$ is continuously differentiable if and only if $f$ is of. A function is said to be continuously differentiable if its derivative is also a continuous function; A function can be continuous at a point, but not be differentiable there. Simply put, differentiable means the derivative exists at every point in its domain. A continuously differentiable function.
polyhedra Continuously Differentiable Functions of Dodecahedron
A continuously differentiable function $f(x)$ is a function whose derivative function. Simply put, differentiable means the derivative exists at every point in its domain. A differentiable function $f$ is continuously differentiable if and only if $f$ is of. A function can be continuous at a point, but not be differentiable there. A function is said to be continuously differentiable if.
Solved A function f(x, y) is called continuously
A function can be continuous at a point, but not be differentiable there. A differentiable function $f$ is continuously differentiable if and only if $f$ is of. A function is said to be continuously differentiable if its derivative is also a continuous function; A continuously differentiable function $f(x)$ is a function whose derivative function. Simply put, differentiable means the derivative.
Solved let's f(x) be a continuously differentiable function
A function is said to be continuously differentiable if its derivative is also a continuous function; A differentiable function $f$ is continuously differentiable if and only if $f$ is of. A function can be continuous at a point, but not be differentiable there. Simply put, differentiable means the derivative exists at every point in its domain. A continuously differentiable function.
Solved Let g be a continuously differentiable function and
Simply put, differentiable means the derivative exists at every point in its domain. A continuously differentiable function $f(x)$ is a function whose derivative function. A function is said to be continuously differentiable if its derivative is also a continuous function; A differentiable function $f$ is continuously differentiable if and only if $f$ is of. A function can be continuous at.
Simply Put, Differentiable Means The Derivative Exists At Every Point In Its Domain.
A function can be continuous at a point, but not be differentiable there. A function is said to be continuously differentiable if its derivative is also a continuous function; A continuously differentiable function $f(x)$ is a function whose derivative function. A differentiable function $f$ is continuously differentiable if and only if $f$ is of.