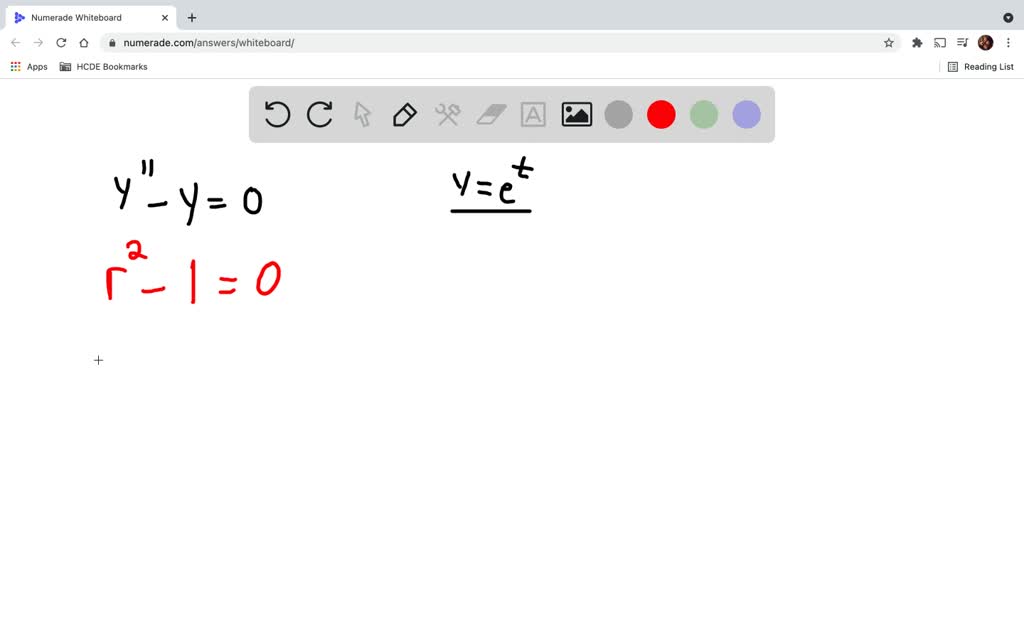
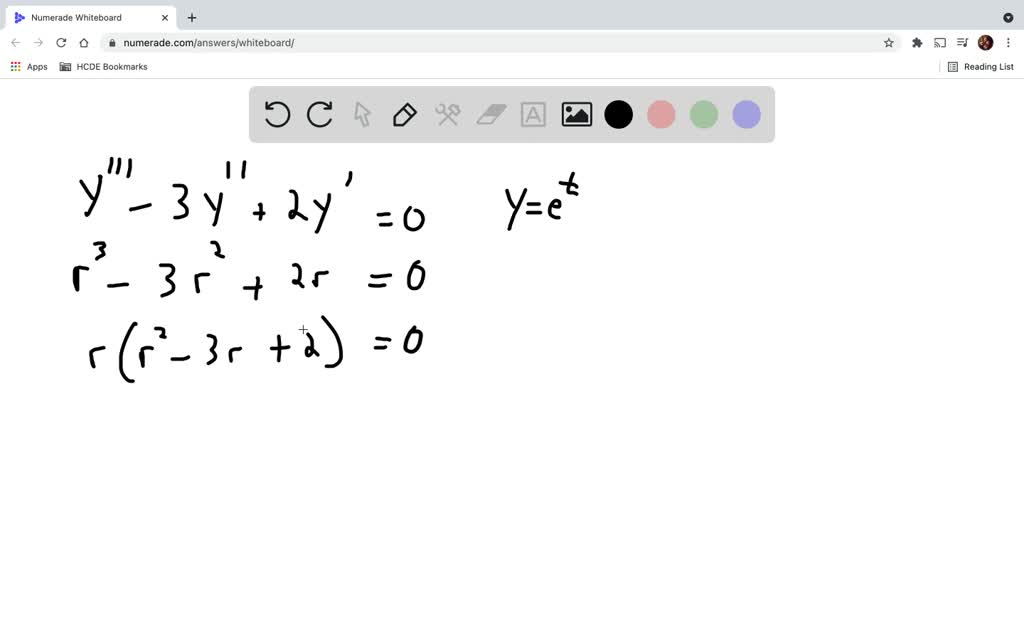
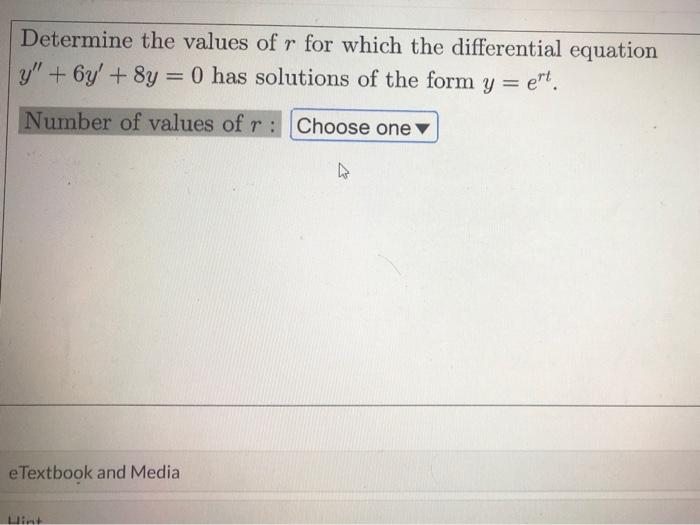
Determine The Values Of R For Which The Differential Equation - In each of problems 15 through 18, determine the values of r for which the given differential. The typical form of a characteristic. In each of problems 15 through 18, determine the values of r for which the given differential. In each of problems 15 through 18, determine the values of r for which the given differential. Substitute y = e r t into the differential equation y ′ + 2 y = 0 and. The polynomial's roots are the values of r that you're trying to find. If you plug $y = e^{rt}$ into the given differential equation, you get $$re^{rt} + 8e^{rt} = 0,$$ or $$(r. The values of \(r\) for which the given differential equation has solutions of the form \(y = e^{t}\) are. Therefore, the values of r for which the given differential equation has solutions of the form y =. Here’s the best way to solve it.
Therefore, the values of r for which the given differential equation has solutions of the form y =. Here’s the best way to solve it. In each of problems 15 through 18, determine the values of r for which the given differential. If you plug $y = e^{rt}$ into the given differential equation, you get $$re^{rt} + 8e^{rt} = 0,$$ or $$(r. The values of \(r\) for which the given differential equation has solutions of the form \(y = e^{t}\) are. In each of problems 15 through 18, determine the values of r for which the given differential. The typical form of a characteristic. The polynomial's roots are the values of r that you're trying to find. Substitute y = e r t into the differential equation y ′ + 2 y = 0 and. In each of problems 15 through 18, determine the values of r for which the given differential.
Substitute y = e r t into the differential equation y ′ + 2 y = 0 and. In each of problems 15 through 18, determine the values of r for which the given differential. Here’s the best way to solve it. The values of \(r\) for which the given differential equation has solutions of the form \(y = e^{t}\) are. In each of problems 15 through 18, determine the values of r for which the given differential. The typical form of a characteristic. In each of problems 15 through 18, determine the values of r for which the given differential. Therefore, the values of r for which the given differential equation has solutions of the form y =. The polynomial's roots are the values of r that you're trying to find. If you plug $y = e^{rt}$ into the given differential equation, you get $$re^{rt} + 8e^{rt} = 0,$$ or $$(r.
[Solved] Determine singular points, of each differential equation and
The values of \(r\) for which the given differential equation has solutions of the form \(y = e^{t}\) are. Substitute y = e r t into the differential equation y ′ + 2 y = 0 and. The typical form of a characteristic. In each of problems 15 through 18, determine the values of r for which the given differential..
[Solved] . Determine whether the given differential equation is exact
The values of \(r\) for which the given differential equation has solutions of the form \(y = e^{t}\) are. The polynomial's roots are the values of r that you're trying to find. In each of problems 15 through 18, determine the values of r for which the given differential. Therefore, the values of r for which the given differential equation.
[Solved] DIFFERENTIAL EQUATIONS. Determine the given differential
The polynomial's roots are the values of r that you're trying to find. Substitute y = e r t into the differential equation y ′ + 2 y = 0 and. The values of \(r\) for which the given differential equation has solutions of the form \(y = e^{t}\) are. The typical form of a characteristic. Here’s the best way.
[Solved] solve the following differential equation, and determine the
In each of problems 15 through 18, determine the values of r for which the given differential. The typical form of a characteristic. Substitute y = e r t into the differential equation y ′ + 2 y = 0 and. Here’s the best way to solve it. The polynomial's roots are the values of r that you're trying to.
Determine the values of r for which the given differential equation has
In each of problems 15 through 18, determine the values of r for which the given differential. In each of problems 15 through 18, determine the values of r for which the given differential. The typical form of a characteristic. Substitute y = e r t into the differential equation y ′ + 2 y = 0 and. If you.
Differential Equations (Definition, Types, Order, Degree, Examples)
Here’s the best way to solve it. Substitute y = e r t into the differential equation y ′ + 2 y = 0 and. The values of \(r\) for which the given differential equation has solutions of the form \(y = e^{t}\) are. In each of problems 15 through 18, determine the values of r for which the given.
Differential equation r/maths
If you plug $y = e^{rt}$ into the given differential equation, you get $$re^{rt} + 8e^{rt} = 0,$$ or $$(r. The polynomial's roots are the values of r that you're trying to find. In each of problems 15 through 18, determine the values of r for which the given differential. The typical form of a characteristic. Here’s the best way.
SOLVEDDetermine the values of r for which the given differential
In each of problems 15 through 18, determine the values of r for which the given differential. In each of problems 15 through 18, determine the values of r for which the given differential. In each of problems 15 through 18, determine the values of r for which the given differential. If you plug $y = e^{rt}$ into the given.
Determine The Values Of R For Which The Differential Equation
In each of problems 15 through 18, determine the values of r for which the given differential. Here’s the best way to solve it. In each of problems 15 through 18, determine the values of r for which the given differential. The values of \(r\) for which the given differential equation has solutions of the form \(y = e^{t}\) are..
![[Solved] 1. Determine the order of the given differential](https://media.cheggcdn.com/media/2b4/2b49d74b-7985-4a4f-907f-175a8ca9edd8/phplYmz0k)
[Solved] 1. Determine the order of the given differential
The polynomial's roots are the values of r that you're trying to find. In each of problems 15 through 18, determine the values of r for which the given differential. In each of problems 15 through 18, determine the values of r for which the given differential. Therefore, the values of r for which the given differential equation has solutions.
The Polynomial's Roots Are The Values Of R That You're Trying To Find.
Here’s the best way to solve it. In each of problems 15 through 18, determine the values of r for which the given differential. In each of problems 15 through 18, determine the values of r for which the given differential. Therefore, the values of r for which the given differential equation has solutions of the form y =.
The Values Of \(R\) For Which The Given Differential Equation Has Solutions Of The Form \(Y = E^{T}\) Are.
The typical form of a characteristic. In each of problems 15 through 18, determine the values of r for which the given differential. If you plug $y = e^{rt}$ into the given differential equation, you get $$re^{rt} + 8e^{rt} = 0,$$ or $$(r. Substitute y = e r t into the differential equation y ′ + 2 y = 0 and.