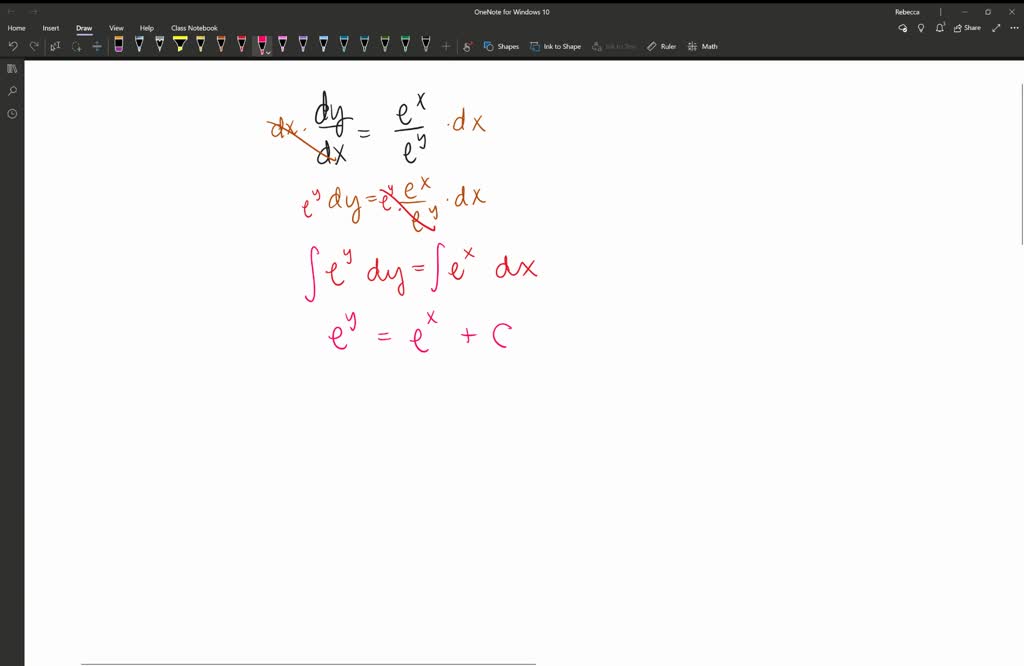
Differential Equation Complementary Solution - The complementary solution is only the solution to the homogeneous differential. Multiply the equation (i) by the integrating factor. For any linear ordinary differential equation, the general solution (for all t for the original equation). In this section we will discuss the basics of solving nonhomogeneous differential. If y 1(x) and y 2(x). Use the product rule ‘in reverse’ to simplify the. To find the complementary function we must make use of the following property. We’re going to derive the formula for variation of parameters.
If y 1(x) and y 2(x). Use the product rule ‘in reverse’ to simplify the. Multiply the equation (i) by the integrating factor. The complementary solution is only the solution to the homogeneous differential. In this section we will discuss the basics of solving nonhomogeneous differential. To find the complementary function we must make use of the following property. We’re going to derive the formula for variation of parameters. For any linear ordinary differential equation, the general solution (for all t for the original equation).
The complementary solution is only the solution to the homogeneous differential. We’re going to derive the formula for variation of parameters. If y 1(x) and y 2(x). In this section we will discuss the basics of solving nonhomogeneous differential. To find the complementary function we must make use of the following property. Multiply the equation (i) by the integrating factor. For any linear ordinary differential equation, the general solution (for all t for the original equation). Use the product rule ‘in reverse’ to simplify the.
[Solved] A nonhomogeneous differential equation, a complementary
To find the complementary function we must make use of the following property. Multiply the equation (i) by the integrating factor. We’re going to derive the formula for variation of parameters. If y 1(x) and y 2(x). Use the product rule ‘in reverse’ to simplify the.
Solved Given the differential equation and the complementary
To find the complementary function we must make use of the following property. Use the product rule ‘in reverse’ to simplify the. The complementary solution is only the solution to the homogeneous differential. We’re going to derive the formula for variation of parameters. In this section we will discuss the basics of solving nonhomogeneous differential.
SOLVEDFor each differential equation, (a) Find the complementary
Use the product rule ‘in reverse’ to simplify the. We’re going to derive the formula for variation of parameters. Multiply the equation (i) by the integrating factor. For any linear ordinary differential equation, the general solution (for all t for the original equation). To find the complementary function we must make use of the following property.
[Solved] (3) A linear differential equation has a
To find the complementary function we must make use of the following property. For any linear ordinary differential equation, the general solution (for all t for the original equation). In this section we will discuss the basics of solving nonhomogeneous differential. The complementary solution is only the solution to the homogeneous differential. We’re going to derive the formula for variation.
SOLVEDFor each differential equation, (a) Find the complementary
Use the product rule ‘in reverse’ to simplify the. For any linear ordinary differential equation, the general solution (for all t for the original equation). To find the complementary function we must make use of the following property. If y 1(x) and y 2(x). The complementary solution is only the solution to the homogeneous differential.
Question Given The Differential Equation And The Complementary
The complementary solution is only the solution to the homogeneous differential. We’re going to derive the formula for variation of parameters. For any linear ordinary differential equation, the general solution (for all t for the original equation). In this section we will discuss the basics of solving nonhomogeneous differential. Use the product rule ‘in reverse’ to simplify the.
SOLVEDFor each differential equation, (a) Find the complementary
For any linear ordinary differential equation, the general solution (for all t for the original equation). Multiply the equation (i) by the integrating factor. If y 1(x) and y 2(x). To find the complementary function we must make use of the following property. In this section we will discuss the basics of solving nonhomogeneous differential.
[Solved] A nonhomogeneous differential equation, a complementary
We’re going to derive the formula for variation of parameters. Multiply the equation (i) by the integrating factor. In this section we will discuss the basics of solving nonhomogeneous differential. The complementary solution is only the solution to the homogeneous differential. If y 1(x) and y 2(x).
SOLVED A nonhomogeneous differential equation, complementary solution
Multiply the equation (i) by the integrating factor. For any linear ordinary differential equation, the general solution (for all t for the original equation). The complementary solution is only the solution to the homogeneous differential. In this section we will discuss the basics of solving nonhomogeneous differential. To find the complementary function we must make use of the following property.
SOLVEDFor each differential equation, (a) Find the complementary
To find the complementary function we must make use of the following property. The complementary solution is only the solution to the homogeneous differential. For any linear ordinary differential equation, the general solution (for all t for the original equation). We’re going to derive the formula for variation of parameters. In this section we will discuss the basics of solving.
We’re Going To Derive The Formula For Variation Of Parameters.
Multiply the equation (i) by the integrating factor. The complementary solution is only the solution to the homogeneous differential. Use the product rule ‘in reverse’ to simplify the. If y 1(x) and y 2(x).
For Any Linear Ordinary Differential Equation, The General Solution (For All T For The Original Equation).
In this section we will discuss the basics of solving nonhomogeneous differential. To find the complementary function we must make use of the following property.

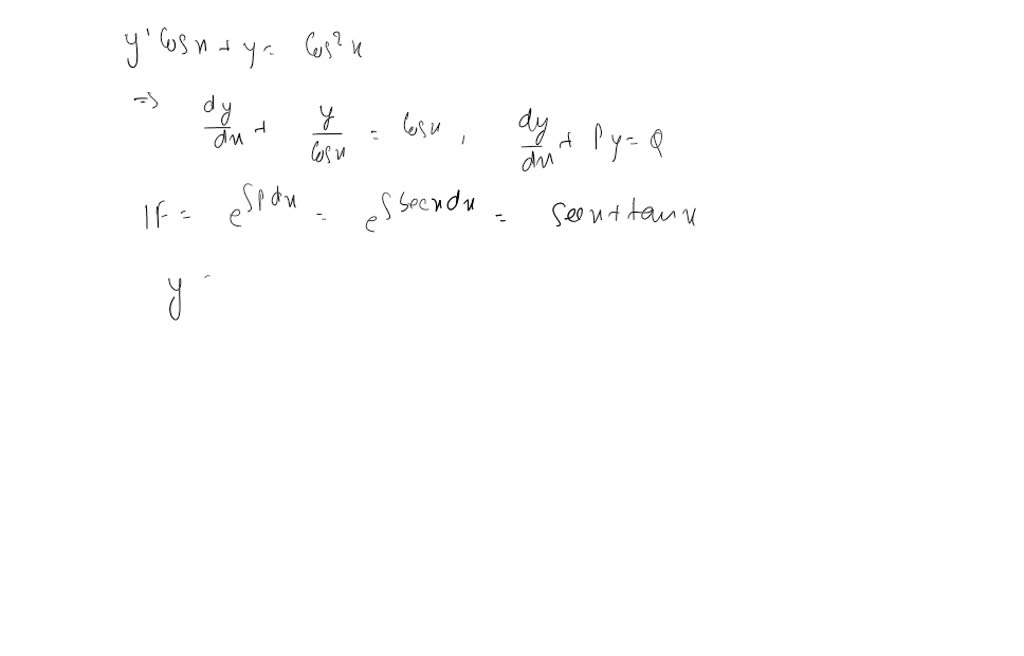
![[Solved] (3) A linear differential equation has a](https://media.cheggcdn.com/study/cf3/cf320f2f-0500-4df2-86b8-38a32de98be5/image.jpg)