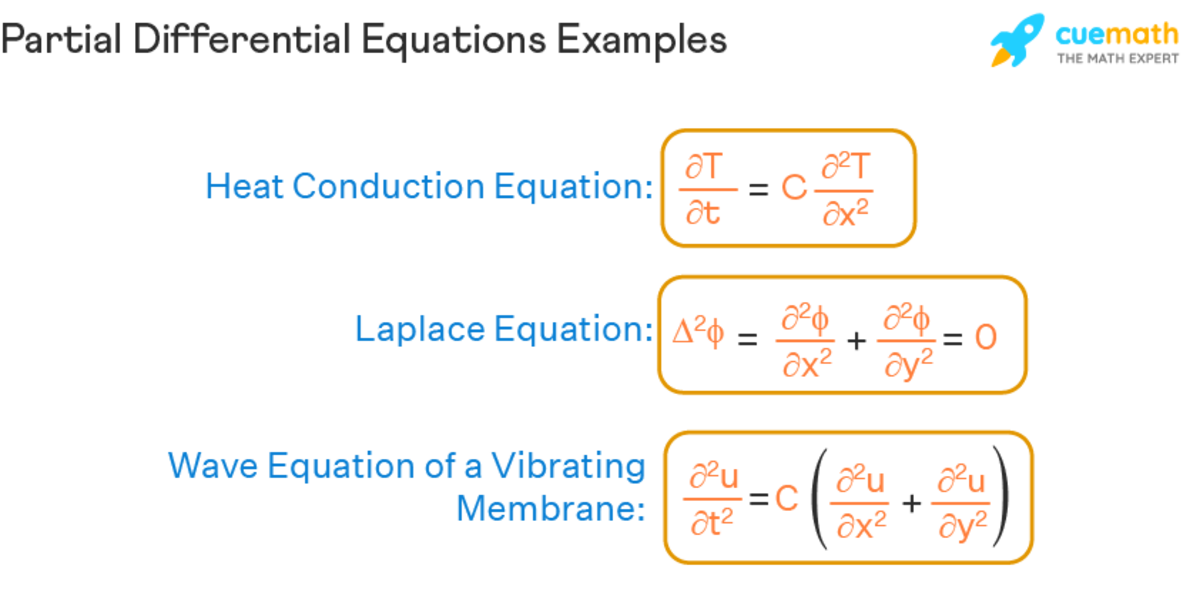
Differential Equations Temperature - The temperature is modeled by the heat equation (seesubsection 7.1for a derivation) @u @t = @2u. Introduction to solving partial differential equations. Heat (or thermal) energy of a body with uniform properties:. Three physical principles are used here. In this section we will do a partial derivation of the heat equation that can be solved. In this section, we explore the method.
Introduction to solving partial differential equations. Heat (or thermal) energy of a body with uniform properties:. The temperature is modeled by the heat equation (seesubsection 7.1for a derivation) @u @t = @2u. In this section, we explore the method. In this section we will do a partial derivation of the heat equation that can be solved. Three physical principles are used here.
Introduction to solving partial differential equations. In this section we will do a partial derivation of the heat equation that can be solved. In this section, we explore the method. The temperature is modeled by the heat equation (seesubsection 7.1for a derivation) @u @t = @2u. Three physical principles are used here. Heat (or thermal) energy of a body with uniform properties:.
22Differential Equation01 Theory PDF Equations Temperature
The temperature is modeled by the heat equation (seesubsection 7.1for a derivation) @u @t = @2u. Three physical principles are used here. In this section we will do a partial derivation of the heat equation that can be solved. Introduction to solving partial differential equations. Heat (or thermal) energy of a body with uniform properties:.
Differential Equations Flashcards Memorang
In this section we will do a partial derivation of the heat equation that can be solved. Introduction to solving partial differential equations. Three physical principles are used here. Heat (or thermal) energy of a body with uniform properties:. The temperature is modeled by the heat equation (seesubsection 7.1for a derivation) @u @t = @2u.
calculus Differential equations temperature change and room
In this section, we explore the method. Introduction to solving partial differential equations. In this section we will do a partial derivation of the heat equation that can be solved. The temperature is modeled by the heat equation (seesubsection 7.1for a derivation) @u @t = @2u. Three physical principles are used here.
Differential Equations Owlcation
Three physical principles are used here. Heat (or thermal) energy of a body with uniform properties:. In this section we will do a partial derivation of the heat equation that can be solved. The temperature is modeled by the heat equation (seesubsection 7.1for a derivation) @u @t = @2u. In this section, we explore the method.
differential equations
The temperature is modeled by the heat equation (seesubsection 7.1for a derivation) @u @t = @2u. In this section, we explore the method. Heat (or thermal) energy of a body with uniform properties:. In this section we will do a partial derivation of the heat equation that can be solved. Three physical principles are used here.
Modelling with Differential Equations Temperature Change
In this section, we explore the method. Three physical principles are used here. Introduction to solving partial differential equations. The temperature is modeled by the heat equation (seesubsection 7.1for a derivation) @u @t = @2u. Heat (or thermal) energy of a body with uniform properties:.
Textbooks Differential Equations Freeup
Introduction to solving partial differential equations. In this section, we explore the method. Heat (or thermal) energy of a body with uniform properties:. Three physical principles are used here. The temperature is modeled by the heat equation (seesubsection 7.1for a derivation) @u @t = @2u.
Differential Equations
In this section, we explore the method. The temperature is modeled by the heat equation (seesubsection 7.1for a derivation) @u @t = @2u. Heat (or thermal) energy of a body with uniform properties:. In this section we will do a partial derivation of the heat equation that can be solved. Introduction to solving partial differential equations.
Worksheet 8 Problems Differential Equation MATH 165 Study
Heat (or thermal) energy of a body with uniform properties:. In this section, we explore the method. In this section we will do a partial derivation of the heat equation that can be solved. The temperature is modeled by the heat equation (seesubsection 7.1for a derivation) @u @t = @2u. Introduction to solving partial differential equations.
Differential Equations Owlcation
Heat (or thermal) energy of a body with uniform properties:. Introduction to solving partial differential equations. The temperature is modeled by the heat equation (seesubsection 7.1for a derivation) @u @t = @2u. In this section, we explore the method. Three physical principles are used here.
The Temperature Is Modeled By The Heat Equation (Seesubsection 7.1For A Derivation) @U @T = @2U.
In this section, we explore the method. Three physical principles are used here. Introduction to solving partial differential equations. Heat (or thermal) energy of a body with uniform properties:.






/aae14611c6e6e45b3bd99783f827f01c.jpg)