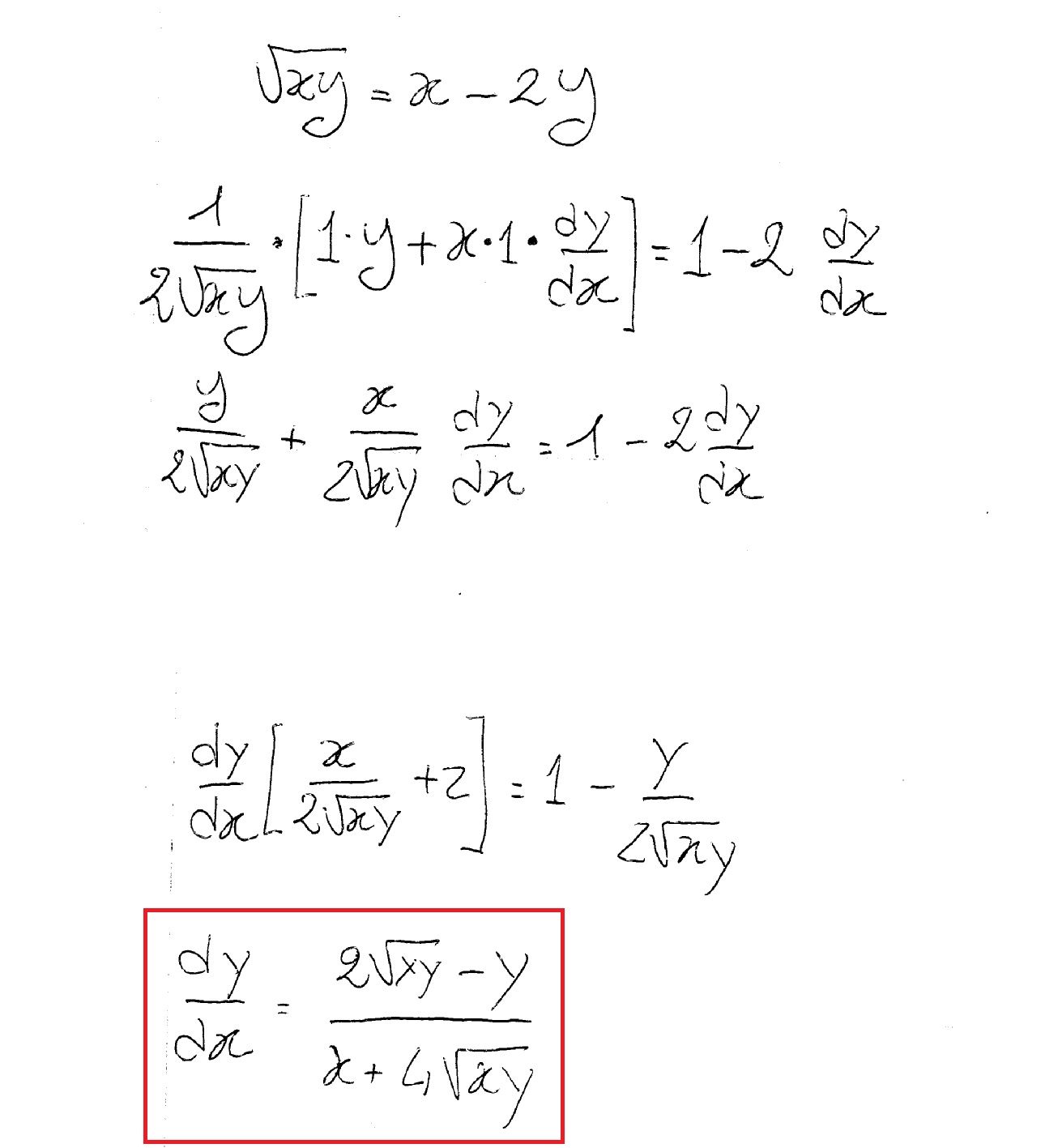Differentiate Sqrt X - How do you find the derivative of y = √x using the definition of derivative? Plugging \sqrt{x} into the definition of the derivative, we multiply the numerator and. $$\frac{d}{dx} \sqrt{f(x)}= \frac{d}{dx} f(x)^\frac{1}{2} $$ then take the derivative and apply the chain rule. Apply the above power rule. This key question has an answer here:. The derivative of \sqrt{x} can also be found using first principles. What is the derivative of square root of x? X^{\msquare} \log_{\msquare} \sqrt{\square} \nthroot[\msquare]{\square} \le \ge \frac{\msquare}{\msquare} \cdot \div: X = x 1 2; Remember that we can rewrite surds like this in index notation.
This key question has an answer here:. X^{\msquare} \log_{\msquare} \sqrt{\square} \nthroot[\msquare]{\square} \le \ge \frac{\msquare}{\msquare} \cdot \div: How do you find the derivative of y = √x using the definition of derivative? X = x 1 2; The derivative of sqrt(x) is 1/(2sqrt(x)). Plugging \sqrt{x} into the definition of the derivative, we multiply the numerator and. If y = x n, then y ′ = n x n − 1. Remember that we can rewrite surds like this in index notation. The derivative of \sqrt{x} can also be found using first principles. What is the derivative of square root of x?
Remember that we can rewrite surds like this in index notation. The derivative of sqrt(x) is 1/(2sqrt(x)). How do you find the derivative of y = √x using the definition of derivative? The derivative of \sqrt{x} can also be found using first principles. $$\frac{d}{dx} \sqrt{f(x)}= \frac{d}{dx} f(x)^\frac{1}{2} $$ then take the derivative and apply the chain rule. X^{\msquare} \log_{\msquare} \sqrt{\square} \nthroot[\msquare]{\square} \le \ge \frac{\msquare}{\msquare} \cdot \div: This key question has an answer here:. Plugging \sqrt{x} into the definition of the derivative, we multiply the numerator and. What is the derivative of square root of x? Apply the above power rule.
calculus Differentiate y = x^{\sqrt{x}} (Simplification
Remember that we can rewrite surds like this in index notation. How do you find the derivative of y = √x using the definition of derivative? Apply the above power rule. The derivative of sqrt(x) is 1/(2sqrt(x)). This key question has an answer here:.
3 Ways to Differentiate the Square Root of X wikiHow
X = x 1 2; Remember that we can rewrite surds like this in index notation. X^{\msquare} \log_{\msquare} \sqrt{\square} \nthroot[\msquare]{\square} \le \ge \frac{\msquare}{\msquare} \cdot \div: The derivative of sqrt(x) is 1/(2sqrt(x)). We rewrite root x using the rule of indices.
Solved Answer Preview Result [sqrt(x+1) (x1)I(x+1)(x1)1)
We rewrite root x using the rule of indices. The derivative of sqrt(x) is 1/(2sqrt(x)). How do you find the derivative of y = √x using the definition of derivative? The derivative of \sqrt{x} can also be found using first principles. $$\frac{d}{dx} \sqrt{f(x)}= \frac{d}{dx} f(x)^\frac{1}{2} $$ then take the derivative and apply the chain rule.
3 Ways to Differentiate the Square Root of X wikiHow
This key question has an answer here:. Apply the above power rule. Remember that we can rewrite surds like this in index notation. If y = x n, then y ′ = n x n − 1. X^{\msquare} \log_{\msquare} \sqrt{\square} \nthroot[\msquare]{\square} \le \ge \frac{\msquare}{\msquare} \cdot \div:
trigonometry About proof \cot^{1}\left(\frac{\sqrt{1+\sin x}+\sqrt
Apply the above power rule. The derivative of sqrt(x) is 1/(2sqrt(x)). Remember that we can rewrite surds like this in index notation. X = x 1 2; X^{\msquare} \log_{\msquare} \sqrt{\square} \nthroot[\msquare]{\square} \le \ge \frac{\msquare}{\msquare} \cdot \div:
How do you differentiate sqrt(xy) = x 2y? Socratic
The derivative of \sqrt{x} can also be found using first principles. We rewrite root x using the rule of indices. Apply the above power rule. X^{\msquare} \log_{\msquare} \sqrt{\square} \nthroot[\msquare]{\square} \le \ge \frac{\msquare}{\msquare} \cdot \div: X = x 1 2;
How do you differentiate y = arccosx + x sqrt(1x^2)? Socratic
X = x 1 2; If y = x n, then y ′ = n x n − 1. Remember that we can rewrite surds like this in index notation. Plugging \sqrt{x} into the definition of the derivative, we multiply the numerator and. We rewrite root x using the rule of indices.
How do you differentiate 5/x^2? Socratic
If y = x n, then y ′ = n x n − 1. We rewrite root x using the rule of indices. Plugging \sqrt{x} into the definition of the derivative, we multiply the numerator and. X = x 1 2; Remember that we can rewrite surds like this in index notation.
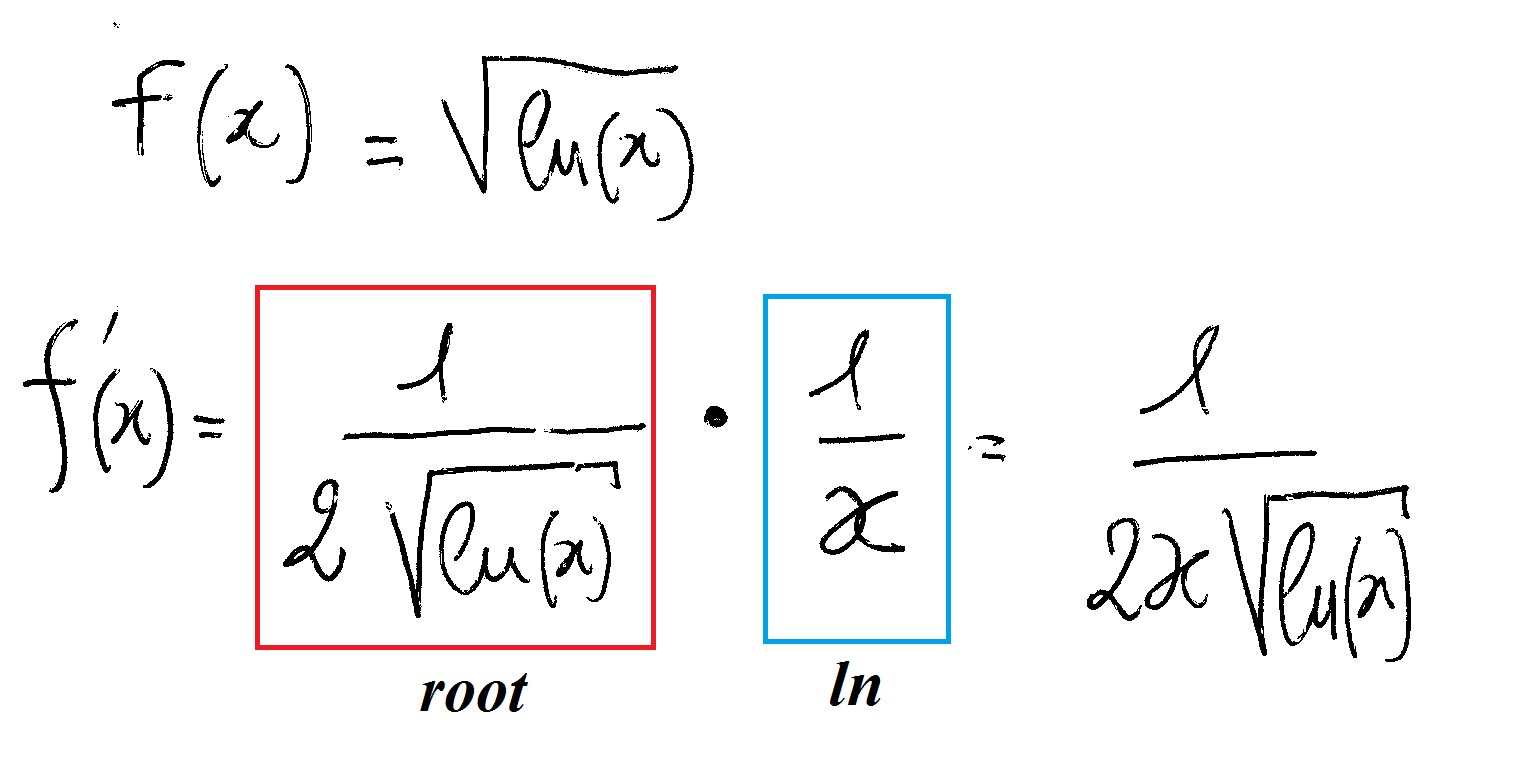
What is the derivative of the sqrt ln x? Socratic
We rewrite root x using the rule of indices. Apply the above power rule. How do you find the derivative of y = √x using the definition of derivative? Plugging \sqrt{x} into the definition of the derivative, we multiply the numerator and. X^{\msquare} \log_{\msquare} \sqrt{\square} \nthroot[\msquare]{\square} \le \ge \frac{\msquare}{\msquare} \cdot \div:
3 Ways to Differentiate the Square Root of X wikiHow
X = x 1 2; This key question has an answer here:. We rewrite root x using the rule of indices. The derivative of \sqrt{x} can also be found using first principles. The derivative of sqrt(x) is 1/(2sqrt(x)).
How Do You Find The Derivative Of Y = √X Using The Definition Of Derivative?
Plugging \sqrt{x} into the definition of the derivative, we multiply the numerator and. This key question has an answer here:. The derivative of sqrt(x) is 1/(2sqrt(x)). The derivative of \sqrt{x} can also be found using first principles.
If Y = X N, Then Y ′ = N X N − 1.
Apply the above power rule. What is the derivative of square root of x? X^{\msquare} \log_{\msquare} \sqrt{\square} \nthroot[\msquare]{\square} \le \ge \frac{\msquare}{\msquare} \cdot \div: We rewrite root x using the rule of indices.
$$\Frac{D}{Dx} \Sqrt{F(X)}= \Frac{D}{Dx} F(X)^\Frac{1}{2} $$ Then Take The Derivative And Apply The Chain Rule.
Remember that we can rewrite surds like this in index notation. X = x 1 2;