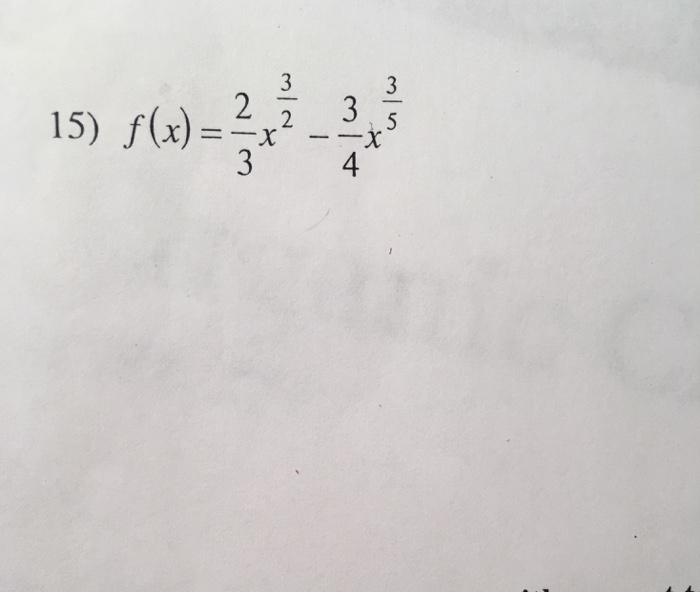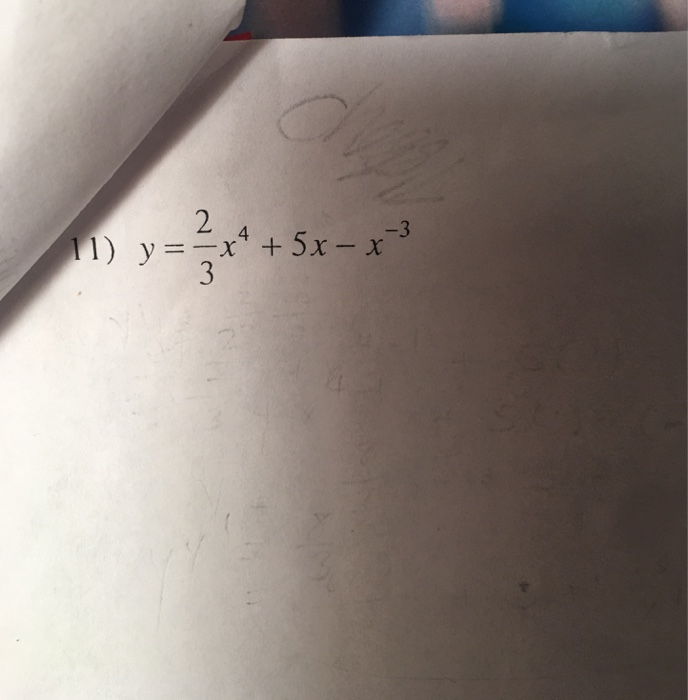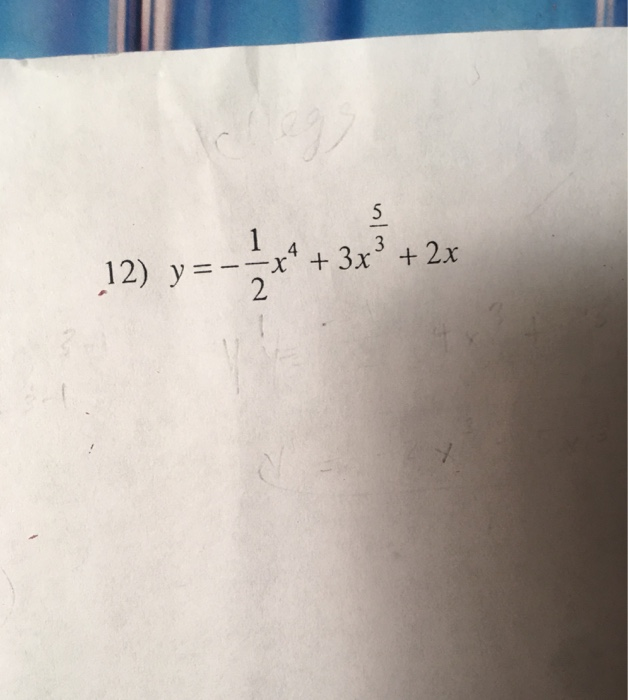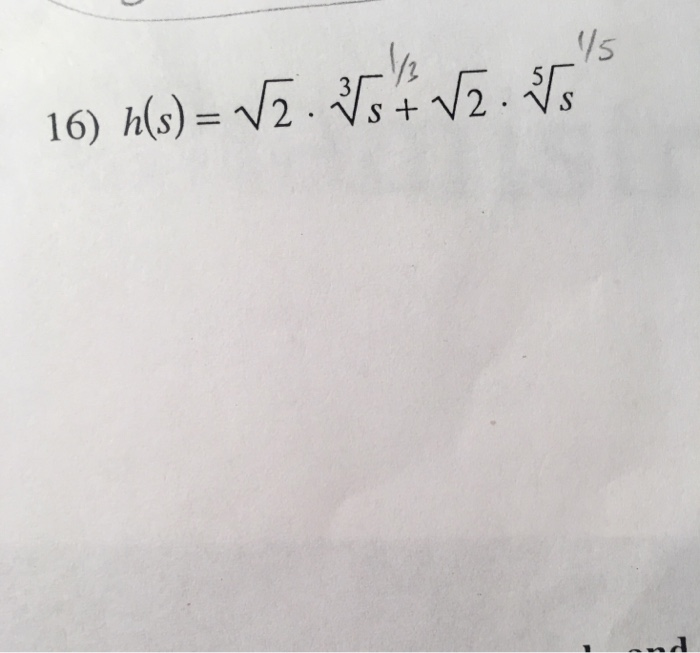Differentiate With Respect To X - At what rate does $f$ change as $x$ changes, in this case it is a constant, $1$. The implicit differentiation calculator will find the first and second derivatives of an implicit function treating either $$$ y $$$ as a function of $$$ x. To differentiate a function of y with respect to x, we differentiate with respect to y and then multiply by dy dx. Key point d dx (f(y)) = d dy (f(y))× dy dx. The derivative with respect to $x$ is:
The implicit differentiation calculator will find the first and second derivatives of an implicit function treating either $$$ y $$$ as a function of $$$ x. At what rate does $f$ change as $x$ changes, in this case it is a constant, $1$. The derivative with respect to $x$ is: To differentiate a function of y with respect to x, we differentiate with respect to y and then multiply by dy dx. Key point d dx (f(y)) = d dy (f(y))× dy dx.
At what rate does $f$ change as $x$ changes, in this case it is a constant, $1$. To differentiate a function of y with respect to x, we differentiate with respect to y and then multiply by dy dx. The implicit differentiation calculator will find the first and second derivatives of an implicit function treating either $$$ y $$$ as a function of $$$ x. Key point d dx (f(y)) = d dy (f(y))× dy dx. The derivative with respect to $x$ is:
Differentiate the following with respect to x (sin x)^x + (cos x)^sinx
The implicit differentiation calculator will find the first and second derivatives of an implicit function treating either $$$ y $$$ as a function of $$$ x. Key point d dx (f(y)) = d dy (f(y))× dy dx. To differentiate a function of y with respect to x, we differentiate with respect to y and then multiply by dy dx. The.
Differentiate with respect to x Maths Continuity and
At what rate does $f$ change as $x$ changes, in this case it is a constant, $1$. Key point d dx (f(y)) = d dy (f(y))× dy dx. The implicit differentiation calculator will find the first and second derivatives of an implicit function treating either $$$ y $$$ as a function of $$$ x. To differentiate a function of y.
Differentiate it with respect to X using general rules Maths Limits
At what rate does $f$ change as $x$ changes, in this case it is a constant, $1$. Key point d dx (f(y)) = d dy (f(y))× dy dx. To differentiate a function of y with respect to x, we differentiate with respect to y and then multiply by dy dx. The implicit differentiation calculator will find the first and second.
Ex 5.2, 8 Differentiate cos (root x) with respect to x
Key point d dx (f(y)) = d dy (f(y))× dy dx. The implicit differentiation calculator will find the first and second derivatives of an implicit function treating either $$$ y $$$ as a function of $$$ x. The derivative with respect to $x$ is: To differentiate a function of y with respect to x, we differentiate with respect to y.
Solved Differentiate The Following Functions With Respect...
The derivative with respect to $x$ is: To differentiate a function of y with respect to x, we differentiate with respect to y and then multiply by dy dx. Key point d dx (f(y)) = d dy (f(y))× dy dx. At what rate does $f$ change as $x$ changes, in this case it is a constant, $1$. The implicit differentiation.
Solved Differentiate each function with respect to x.
To differentiate a function of y with respect to x, we differentiate with respect to y and then multiply by dy dx. The derivative with respect to $x$ is: Key point d dx (f(y)) = d dy (f(y))× dy dx. The implicit differentiation calculator will find the first and second derivatives of an implicit function treating either $$$ y $$$.
Solved Differentiate each function with respect to x.
The derivative with respect to $x$ is: Key point d dx (f(y)) = d dy (f(y))× dy dx. To differentiate a function of y with respect to x, we differentiate with respect to y and then multiply by dy dx. The implicit differentiation calculator will find the first and second derivatives of an implicit function treating either $$$ y $$$.
Differentiate the following function with respect to x. 2x^2 + 3x + 4x
The derivative with respect to $x$ is: The implicit differentiation calculator will find the first and second derivatives of an implicit function treating either $$$ y $$$ as a function of $$$ x. To differentiate a function of y with respect to x, we differentiate with respect to y and then multiply by dy dx. Key point d dx (f(y)).
Solved Differentiate each function with respect to x.
The derivative with respect to $x$ is: At what rate does $f$ change as $x$ changes, in this case it is a constant, $1$. To differentiate a function of y with respect to x, we differentiate with respect to y and then multiply by dy dx. Key point d dx (f(y)) = d dy (f(y))× dy dx. The implicit differentiation.
Solved Differentiate each function with respect to x.
Key point d dx (f(y)) = d dy (f(y))× dy dx. At what rate does $f$ change as $x$ changes, in this case it is a constant, $1$. The derivative with respect to $x$ is: The implicit differentiation calculator will find the first and second derivatives of an implicit function treating either $$$ y $$$ as a function of $$$.
The Implicit Differentiation Calculator Will Find The First And Second Derivatives Of An Implicit Function Treating Either $$$ Y $$$ As A Function Of $$$ X.
At what rate does $f$ change as $x$ changes, in this case it is a constant, $1$. Key point d dx (f(y)) = d dy (f(y))× dy dx. To differentiate a function of y with respect to x, we differentiate with respect to y and then multiply by dy dx. The derivative with respect to $x$ is: