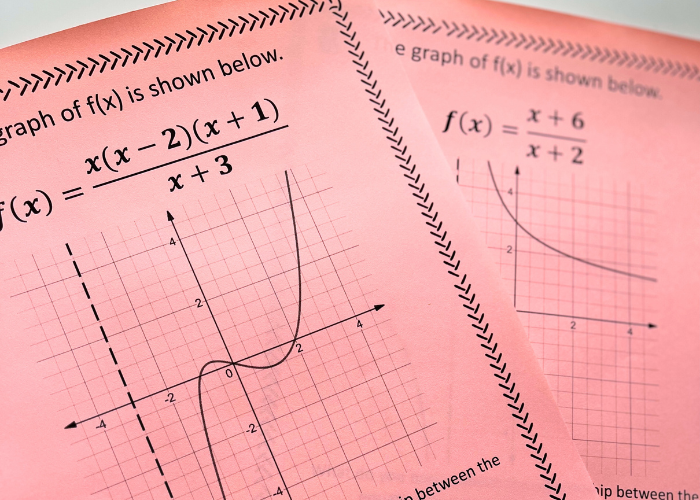
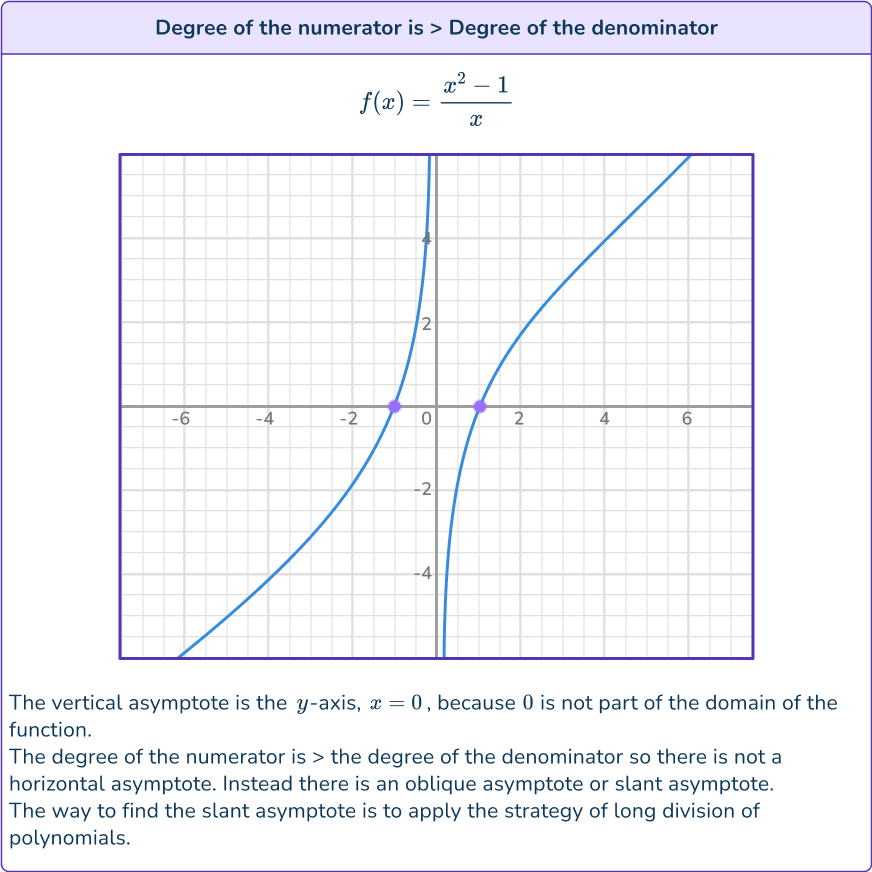
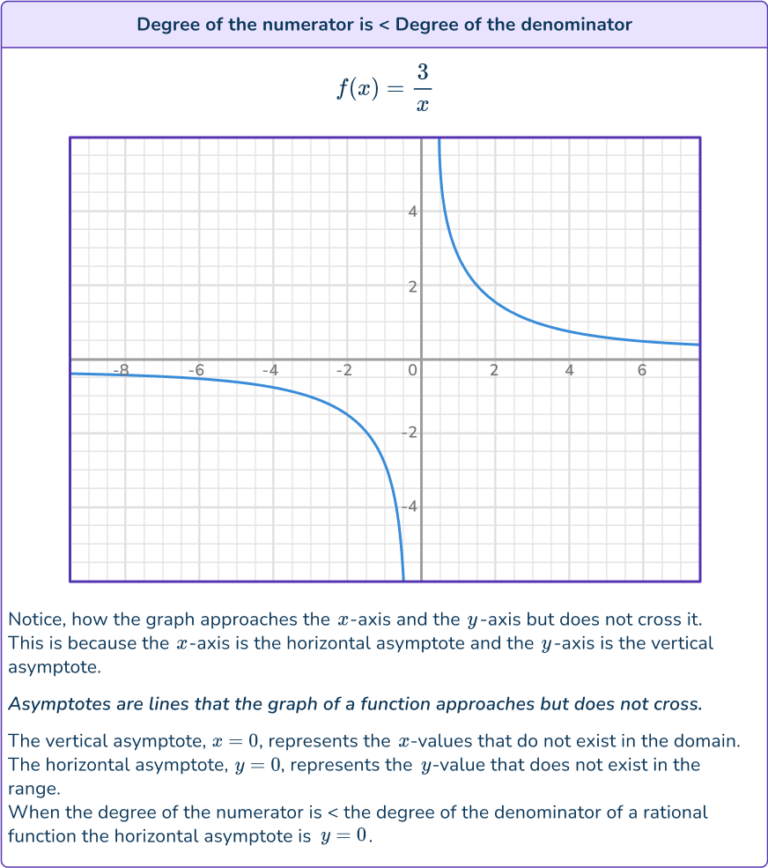
Differentiating Rational Functions - Differentiating rational functions, with discussion and proofs of the constant, sum, product, quotient, and power rules. Differentiating rational functions, with discussion and proofs of the constant, sum, product, quotient, and power rules. Remember that a rational function \(h(x)\) can be expressed in such a way that \(h(x)=\frac{f(x)}{g(x)},\) where \(f(x)\) and. It is seen as crucial knowledge in. We actually get most useful functions by starting. This function (and any other rational function) can be differentiated. You should practice finding the derivatives of polynomials and of rational functions using these rules until you feel comfortable with them. Rational functions are an important and useful class of functions, but there are others. The derivative of a rational function measures how the function changes at any given point.
This function (and any other rational function) can be differentiated. Differentiating rational functions, with discussion and proofs of the constant, sum, product, quotient, and power rules. Remember that a rational function \(h(x)\) can be expressed in such a way that \(h(x)=\frac{f(x)}{g(x)},\) where \(f(x)\) and. You should practice finding the derivatives of polynomials and of rational functions using these rules until you feel comfortable with them. The derivative of a rational function measures how the function changes at any given point. Rational functions are an important and useful class of functions, but there are others. We actually get most useful functions by starting. Differentiating rational functions, with discussion and proofs of the constant, sum, product, quotient, and power rules. It is seen as crucial knowledge in.
You should practice finding the derivatives of polynomials and of rational functions using these rules until you feel comfortable with them. Differentiating rational functions, with discussion and proofs of the constant, sum, product, quotient, and power rules. It is seen as crucial knowledge in. The derivative of a rational function measures how the function changes at any given point. This function (and any other rational function) can be differentiated. Rational functions are an important and useful class of functions, but there are others. Remember that a rational function \(h(x)\) can be expressed in such a way that \(h(x)=\frac{f(x)}{g(x)},\) where \(f(x)\) and. Differentiating rational functions, with discussion and proofs of the constant, sum, product, quotient, and power rules. We actually get most useful functions by starting.
Rational Functions Archives Mathy Mrs. J
This function (and any other rational function) can be differentiated. The derivative of a rational function measures how the function changes at any given point. It is seen as crucial knowledge in. Differentiating rational functions, with discussion and proofs of the constant, sum, product, quotient, and power rules. You should practice finding the derivatives of polynomials and of rational functions.
Solved It is a common misconception when differentiating
It is seen as crucial knowledge in. Differentiating rational functions, with discussion and proofs of the constant, sum, product, quotient, and power rules. This function (and any other rational function) can be differentiated. Rational functions are an important and useful class of functions, but there are others. Differentiating rational functions, with discussion and proofs of the constant, sum, product, quotient,.
Rational Functions Math Steps, Examples & Questions
It is seen as crucial knowledge in. This function (and any other rational function) can be differentiated. Rational functions are an important and useful class of functions, but there are others. The derivative of a rational function measures how the function changes at any given point. Differentiating rational functions, with discussion and proofs of the constant, sum, product, quotient, and.
Graphing rational functions PPT
Remember that a rational function \(h(x)\) can be expressed in such a way that \(h(x)=\frac{f(x)}{g(x)},\) where \(f(x)\) and. You should practice finding the derivatives of polynomials and of rational functions using these rules until you feel comfortable with them. Differentiating rational functions, with discussion and proofs of the constant, sum, product, quotient, and power rules. The derivative of a rational.
10 Surprising Reallife Examples Of Rational Functions Number Dyslexia
We actually get most useful functions by starting. Rational functions are an important and useful class of functions, but there are others. The derivative of a rational function measures how the function changes at any given point. Remember that a rational function \(h(x)\) can be expressed in such a way that \(h(x)=\frac{f(x)}{g(x)},\) where \(f(x)\) and. It is seen as crucial.
RationalFunctionsEquationsandInequalities.pptx Free Download
Remember that a rational function \(h(x)\) can be expressed in such a way that \(h(x)=\frac{f(x)}{g(x)},\) where \(f(x)\) and. Differentiating rational functions, with discussion and proofs of the constant, sum, product, quotient, and power rules. Differentiating rational functions, with discussion and proofs of the constant, sum, product, quotient, and power rules. It is seen as crucial knowledge in. We actually get.
Rational Functions Math Steps, Examples & Questions
Rational functions are an important and useful class of functions, but there are others. We actually get most useful functions by starting. You should practice finding the derivatives of polynomials and of rational functions using these rules until you feel comfortable with them. Remember that a rational function \(h(x)\) can be expressed in such a way that \(h(x)=\frac{f(x)}{g(x)},\) where \(f(x)\).
Rational Functions Unit Bundle Clark Creative Education
Rational functions are an important and useful class of functions, but there are others. We actually get most useful functions by starting. This function (and any other rational function) can be differentiated. Differentiating rational functions, with discussion and proofs of the constant, sum, product, quotient, and power rules. It is seen as crucial knowledge in.
Rational Functions Studocu
We actually get most useful functions by starting. This function (and any other rational function) can be differentiated. Remember that a rational function \(h(x)\) can be expressed in such a way that \(h(x)=\frac{f(x)}{g(x)},\) where \(f(x)\) and. Rational functions are an important and useful class of functions, but there are others. You should practice finding the derivatives of polynomials and of.
Rational Functions PDF Asymptote Equations
This function (and any other rational function) can be differentiated. Differentiating rational functions, with discussion and proofs of the constant, sum, product, quotient, and power rules. It is seen as crucial knowledge in. Differentiating rational functions, with discussion and proofs of the constant, sum, product, quotient, and power rules. Rational functions are an important and useful class of functions, but.
The Derivative Of A Rational Function Measures How The Function Changes At Any Given Point.
Differentiating rational functions, with discussion and proofs of the constant, sum, product, quotient, and power rules. You should practice finding the derivatives of polynomials and of rational functions using these rules until you feel comfortable with them. It is seen as crucial knowledge in. Remember that a rational function \(h(x)\) can be expressed in such a way that \(h(x)=\frac{f(x)}{g(x)},\) where \(f(x)\) and.
Rational Functions Are An Important And Useful Class Of Functions, But There Are Others.
We actually get most useful functions by starting. This function (and any other rational function) can be differentiated. Differentiating rational functions, with discussion and proofs of the constant, sum, product, quotient, and power rules.