Differentiation Formula Pdf - 𝑓𝑓(𝑥𝑥) ± 𝑔𝑔(𝑥𝑥) ′ = 𝑓𝑓′(𝑥𝑥) ± 𝑔𝑔′(𝑥𝑥) 2. D dx (xn) = nxn−1 z xn dx = 1 n+1 xn+1. Differentiation formulas derivatives of basic functions derivatives of logarithmic and exponential functions If y = c, = (c) = 0 dx d dx dy where ‘c’ is any arbitrary. Basic differentiation and integration formulas # 1 derivatives # 2 antiderivatives memorize. The derivative of a constant is equal to zero. General rules of differentiation 1.
D dx (xn) = nxn−1 z xn dx = 1 n+1 xn+1. If y = c, = (c) = 0 dx d dx dy where ‘c’ is any arbitrary. 𝑓𝑓(𝑥𝑥) ± 𝑔𝑔(𝑥𝑥) ′ = 𝑓𝑓′(𝑥𝑥) ± 𝑔𝑔′(𝑥𝑥) 2. Basic differentiation and integration formulas # 1 derivatives # 2 antiderivatives memorize. General rules of differentiation 1. Differentiation formulas derivatives of basic functions derivatives of logarithmic and exponential functions The derivative of a constant is equal to zero.
Differentiation formulas derivatives of basic functions derivatives of logarithmic and exponential functions The derivative of a constant is equal to zero. Basic differentiation and integration formulas # 1 derivatives # 2 antiderivatives memorize. D dx (xn) = nxn−1 z xn dx = 1 n+1 xn+1. General rules of differentiation 1. If y = c, = (c) = 0 dx d dx dy where ‘c’ is any arbitrary. 𝑓𝑓(𝑥𝑥) ± 𝑔𝑔(𝑥𝑥) ′ = 𝑓𝑓′(𝑥𝑥) ± 𝑔𝑔′(𝑥𝑥) 2.
Differentiation Formula for Trigonometric Functions
D dx (xn) = nxn−1 z xn dx = 1 n+1 xn+1. Differentiation formulas derivatives of basic functions derivatives of logarithmic and exponential functions If y = c, = (c) = 0 dx d dx dy where ‘c’ is any arbitrary. Basic differentiation and integration formulas # 1 derivatives # 2 antiderivatives memorize. General rules of differentiation 1.
SOLUTION Differentiation and integration formulas Studypool
General rules of differentiation 1. The derivative of a constant is equal to zero. D dx (xn) = nxn−1 z xn dx = 1 n+1 xn+1. If y = c, = (c) = 0 dx d dx dy where ‘c’ is any arbitrary. Differentiation formulas derivatives of basic functions derivatives of logarithmic and exponential functions
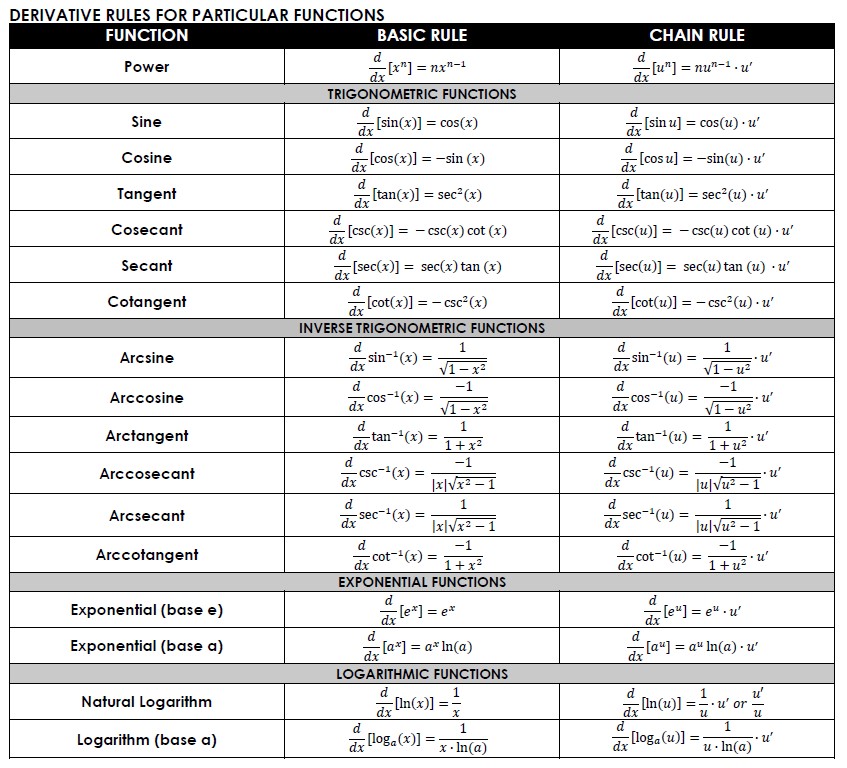
Free Printable Derivatives Formula Chart (PDF) Math Love, 51 OFF
𝑓𝑓(𝑥𝑥) ± 𝑔𝑔(𝑥𝑥) ′ = 𝑓𝑓′(𝑥𝑥) ± 𝑔𝑔′(𝑥𝑥) 2. If y = c, = (c) = 0 dx d dx dy where ‘c’ is any arbitrary. D dx (xn) = nxn−1 z xn dx = 1 n+1 xn+1. General rules of differentiation 1. Differentiation formulas derivatives of basic functions derivatives of logarithmic and exponential functions
SOLUTION Differentiation formulas for JEE and NEET Studypool
𝑓𝑓(𝑥𝑥) ± 𝑔𝑔(𝑥𝑥) ′ = 𝑓𝑓′(𝑥𝑥) ± 𝑔𝑔′(𝑥𝑥) 2. D dx (xn) = nxn−1 z xn dx = 1 n+1 xn+1. General rules of differentiation 1. Basic differentiation and integration formulas # 1 derivatives # 2 antiderivatives memorize. The derivative of a constant is equal to zero.
Differentiation formulas for class 12 PDF Class 12 easy
Basic differentiation and integration formulas # 1 derivatives # 2 antiderivatives memorize. General rules of differentiation 1. If y = c, = (c) = 0 dx d dx dy where ‘c’ is any arbitrary. The derivative of a constant is equal to zero. 𝑓𝑓(𝑥𝑥) ± 𝑔𝑔(𝑥𝑥) ′ = 𝑓𝑓′(𝑥𝑥) ± 𝑔𝑔′(𝑥𝑥) 2.
SOLUTION Integration and differentiation formula sheet Studypool
Differentiation formulas derivatives of basic functions derivatives of logarithmic and exponential functions The derivative of a constant is equal to zero. If y = c, = (c) = 0 dx d dx dy where ‘c’ is any arbitrary. General rules of differentiation 1. D dx (xn) = nxn−1 z xn dx = 1 n+1 xn+1.
SOLUTION Differentiation formulas pdf Studypool
Differentiation formulas derivatives of basic functions derivatives of logarithmic and exponential functions Basic differentiation and integration formulas # 1 derivatives # 2 antiderivatives memorize. General rules of differentiation 1. D dx (xn) = nxn−1 z xn dx = 1 n+1 xn+1. The derivative of a constant is equal to zero.
Maths Differentiation Formula PDF
The derivative of a constant is equal to zero. General rules of differentiation 1. D dx (xn) = nxn−1 z xn dx = 1 n+1 xn+1. Differentiation formulas derivatives of basic functions derivatives of logarithmic and exponential functions 𝑓𝑓(𝑥𝑥) ± 𝑔𝑔(𝑥𝑥) ′ = 𝑓𝑓′(𝑥𝑥) ± 𝑔𝑔′(𝑥𝑥) 2.
TD n 3 Différentiabilité
Differentiation formulas derivatives of basic functions derivatives of logarithmic and exponential functions 𝑓𝑓(𝑥𝑥) ± 𝑔𝑔(𝑥𝑥) ′ = 𝑓𝑓′(𝑥𝑥) ± 𝑔𝑔′(𝑥𝑥) 2. If y = c, = (c) = 0 dx d dx dy where ‘c’ is any arbitrary. General rules of differentiation 1. D dx (xn) = nxn−1 z xn dx = 1 n+1 xn+1.
Differentiation formulas Artofit
General rules of differentiation 1. D dx (xn) = nxn−1 z xn dx = 1 n+1 xn+1. Basic differentiation and integration formulas # 1 derivatives # 2 antiderivatives memorize. If y = c, = (c) = 0 dx d dx dy where ‘c’ is any arbitrary. The derivative of a constant is equal to zero.
General Rules Of Differentiation 1.
D dx (xn) = nxn−1 z xn dx = 1 n+1 xn+1. Basic differentiation and integration formulas # 1 derivatives # 2 antiderivatives memorize. Differentiation formulas derivatives of basic functions derivatives of logarithmic and exponential functions If y = c, = (c) = 0 dx d dx dy where ‘c’ is any arbitrary.
The Derivative Of A Constant Is Equal To Zero.
𝑓𝑓(𝑥𝑥) ± 𝑔𝑔(𝑥𝑥) ′ = 𝑓𝑓′(𝑥𝑥) ± 𝑔𝑔′(𝑥𝑥) 2.