Differentiation Of Arctan X - Derivative of arctan(x) let’s use our formula for the derivative of an inverse function to find the deriva tive of the inverse of the tangent. Each of the functions to be differentiated is a composition,. $\dfrac {\map \d {\arctan x} } {\d x} = \dfrac 1 {1 + x^2}$. Let $\arctan x$ be the arctangent of $x$.
$\dfrac {\map \d {\arctan x} } {\d x} = \dfrac 1 {1 + x^2}$. Let $\arctan x$ be the arctangent of $x$. Each of the functions to be differentiated is a composition,. Derivative of arctan(x) let’s use our formula for the derivative of an inverse function to find the deriva tive of the inverse of the tangent.
$\dfrac {\map \d {\arctan x} } {\d x} = \dfrac 1 {1 + x^2}$. Let $\arctan x$ be the arctangent of $x$. Derivative of arctan(x) let’s use our formula for the derivative of an inverse function to find the deriva tive of the inverse of the tangent. Each of the functions to be differentiated is a composition,.
3. Let d3(x,y)=∣arctan(x)−arctan(y)∣ for x,y∈R. (a).
Each of the functions to be differentiated is a composition,. Let $\arctan x$ be the arctangent of $x$. Derivative of arctan(x) let’s use our formula for the derivative of an inverse function to find the deriva tive of the inverse of the tangent. $\dfrac {\map \d {\arctan x} } {\d x} = \dfrac 1 {1 + x^2}$.
Derivative of arctan(x) (Inverse tangent) Detailed Lesson
$\dfrac {\map \d {\arctan x} } {\d x} = \dfrac 1 {1 + x^2}$. Each of the functions to be differentiated is a composition,. Let $\arctan x$ be the arctangent of $x$. Derivative of arctan(x) let’s use our formula for the derivative of an inverse function to find the deriva tive of the inverse of the tangent.
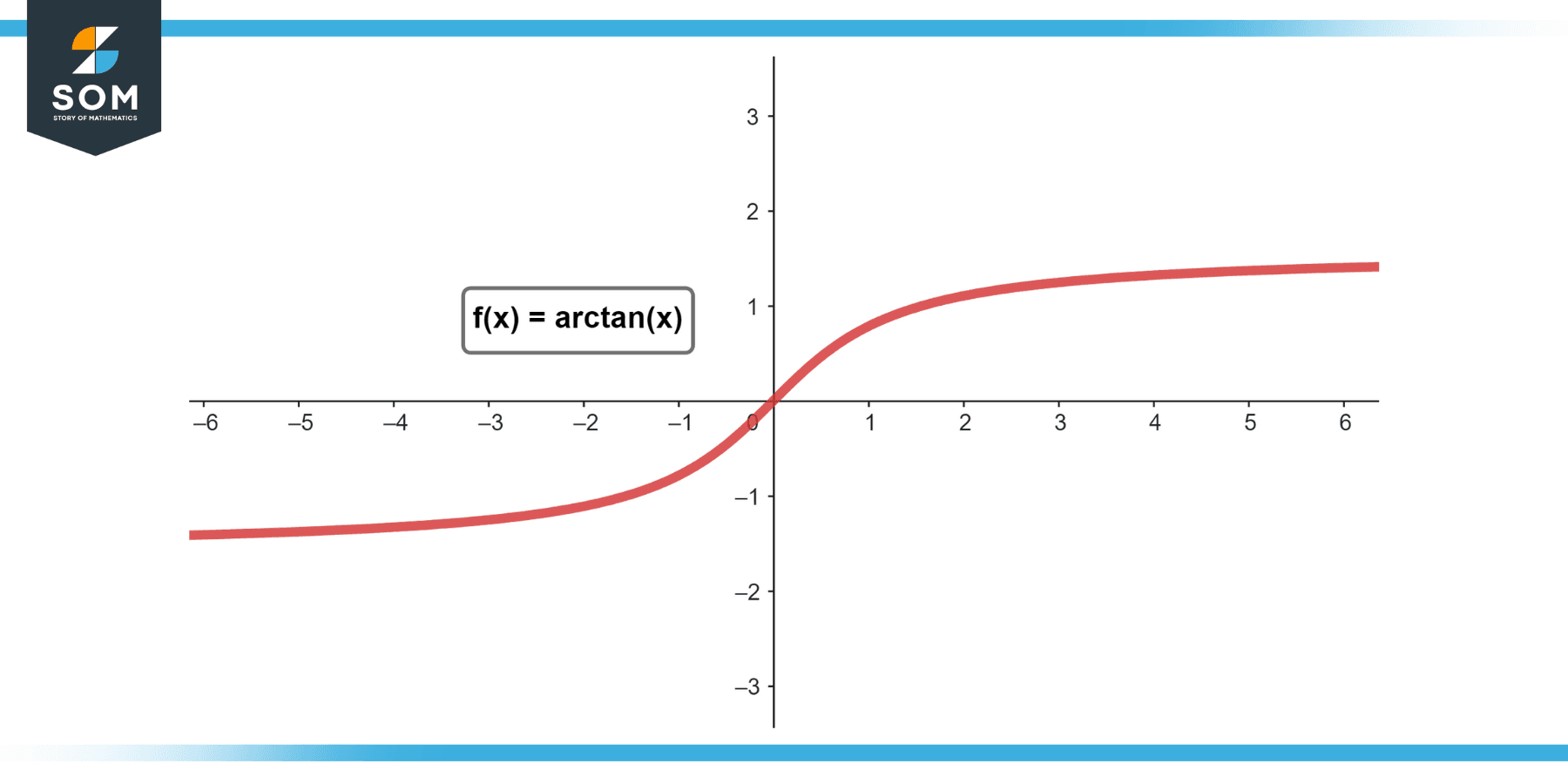
Arctan Formula, Graph, Identities, Domain and Range Arctan x
Let $\arctan x$ be the arctangent of $x$. $\dfrac {\map \d {\arctan x} } {\d x} = \dfrac 1 {1 + x^2}$. Derivative of arctan(x) let’s use our formula for the derivative of an inverse function to find the deriva tive of the inverse of the tangent. Each of the functions to be differentiated is a composition,.
Prove each differentiation formula. (a) Prove that arctan x+arctany
$\dfrac {\map \d {\arctan x} } {\d x} = \dfrac 1 {1 + x^2}$. Each of the functions to be differentiated is a composition,. Let $\arctan x$ be the arctangent of $x$. Derivative of arctan(x) let’s use our formula for the derivative of an inverse function to find the deriva tive of the inverse of the tangent.
Derivative of Arctan Formula & Examples Education Spike
$\dfrac {\map \d {\arctan x} } {\d x} = \dfrac 1 {1 + x^2}$. Derivative of arctan(x) let’s use our formula for the derivative of an inverse function to find the deriva tive of the inverse of the tangent. Each of the functions to be differentiated is a composition,. Let $\arctan x$ be the arctangent of $x$.
Sec(arctan(x)) not working properly Bug Reports Computation Layer
$\dfrac {\map \d {\arctan x} } {\d x} = \dfrac 1 {1 + x^2}$. Derivative of arctan(x) let’s use our formula for the derivative of an inverse function to find the deriva tive of the inverse of the tangent. Each of the functions to be differentiated is a composition,. Let $\arctan x$ be the arctangent of $x$.
Numpy arctan2 Find elementwise arctan of x1/x2
$\dfrac {\map \d {\arctan x} } {\d x} = \dfrac 1 {1 + x^2}$. Derivative of arctan(x) let’s use our formula for the derivative of an inverse function to find the deriva tive of the inverse of the tangent. Let $\arctan x$ be the arctangent of $x$. Each of the functions to be differentiated is a composition,.
arctan(0) Definition, Applications, and Examples
Each of the functions to be differentiated is a composition,. $\dfrac {\map \d {\arctan x} } {\d x} = \dfrac 1 {1 + x^2}$. Let $\arctan x$ be the arctangent of $x$. Derivative of arctan(x) let’s use our formula for the derivative of an inverse function to find the deriva tive of the inverse of the tangent.
Solved 3. Let I=arctan(x)/x(dx). (a) Find the Taylor
Let $\arctan x$ be the arctangent of $x$. Each of the functions to be differentiated is a composition,. $\dfrac {\map \d {\arctan x} } {\d x} = \dfrac 1 {1 + x^2}$. Derivative of arctan(x) let’s use our formula for the derivative of an inverse function to find the deriva tive of the inverse of the tangent.
Derivative of arctan(x)
Each of the functions to be differentiated is a composition,. Let $\arctan x$ be the arctangent of $x$. $\dfrac {\map \d {\arctan x} } {\d x} = \dfrac 1 {1 + x^2}$. Derivative of arctan(x) let’s use our formula for the derivative of an inverse function to find the deriva tive of the inverse of the tangent.
Each Of The Functions To Be Differentiated Is A Composition,.
$\dfrac {\map \d {\arctan x} } {\d x} = \dfrac 1 {1 + x^2}$. Let $\arctan x$ be the arctangent of $x$. Derivative of arctan(x) let’s use our formula for the derivative of an inverse function to find the deriva tive of the inverse of the tangent.