Differentiation Of Bessel Function - Bessel function jn ode representation (y(x)=j n(x) is a solution to this ode) x2y xx +xy x +(x 2 −n2)y =0 (1) series. Let’s begin with a derivative. We begin with a derivation of the bessel functions ja(x) and ya(x), which are two solutions to bessel's di erential equation. There are numerous identities involving bessel functions which may now be generated using the above definitions. Integrating the differential relations leads to the integral relations.
Let’s begin with a derivative. We begin with a derivation of the bessel functions ja(x) and ya(x), which are two solutions to bessel's di erential equation. Bessel function jn ode representation (y(x)=j n(x) is a solution to this ode) x2y xx +xy x +(x 2 −n2)y =0 (1) series. Integrating the differential relations leads to the integral relations. There are numerous identities involving bessel functions which may now be generated using the above definitions.
Let’s begin with a derivative. There are numerous identities involving bessel functions which may now be generated using the above definitions. Integrating the differential relations leads to the integral relations. Bessel function jn ode representation (y(x)=j n(x) is a solution to this ode) x2y xx +xy x +(x 2 −n2)y =0 (1) series. We begin with a derivation of the bessel functions ja(x) and ya(x), which are two solutions to bessel's di erential equation.
Bessel Function Series Solution
We begin with a derivation of the bessel functions ja(x) and ya(x), which are two solutions to bessel's di erential equation. Bessel function jn ode representation (y(x)=j n(x) is a solution to this ode) x2y xx +xy x +(x 2 −n2)y =0 (1) series. Let’s begin with a derivative. There are numerous identities involving bessel functions which may now be.
integration product of bessel function integral Mathematics Stack
Integrating the differential relations leads to the integral relations. Bessel function jn ode representation (y(x)=j n(x) is a solution to this ode) x2y xx +xy x +(x 2 −n2)y =0 (1) series. There are numerous identities involving bessel functions which may now be generated using the above definitions. Let’s begin with a derivative. We begin with a derivation of the.
Modified Bessel Function Table
We begin with a derivation of the bessel functions ja(x) and ya(x), which are two solutions to bessel's di erential equation. Bessel function jn ode representation (y(x)=j n(x) is a solution to this ode) x2y xx +xy x +(x 2 −n2)y =0 (1) series. Integrating the differential relations leads to the integral relations. There are numerous identities involving bessel functions.
Bessel Function Of Second Kind Skedbooks
Let’s begin with a derivative. Integrating the differential relations leads to the integral relations. We begin with a derivation of the bessel functions ja(x) and ya(x), which are two solutions to bessel's di erential equation. Bessel function jn ode representation (y(x)=j n(x) is a solution to this ode) x2y xx +xy x +(x 2 −n2)y =0 (1) series. There are.
Zeroth‐order Bessel function of the first kind. Download Scientific
Integrating the differential relations leads to the integral relations. There are numerous identities involving bessel functions which may now be generated using the above definitions. We begin with a derivation of the bessel functions ja(x) and ya(x), which are two solutions to bessel's di erential equation. Bessel function jn ode representation (y(x)=j n(x) is a solution to this ode) x2y.
Generating Function For Bessel Function
Bessel function jn ode representation (y(x)=j n(x) is a solution to this ode) x2y xx +xy x +(x 2 −n2)y =0 (1) series. We begin with a derivation of the bessel functions ja(x) and ya(x), which are two solutions to bessel's di erential equation. Let’s begin with a derivative. There are numerous identities involving bessel functions which may now be.
Properties Of Bessel Function Skedbooks
Integrating the differential relations leads to the integral relations. There are numerous identities involving bessel functions which may now be generated using the above definitions. Let’s begin with a derivative. We begin with a derivation of the bessel functions ja(x) and ya(x), which are two solutions to bessel's di erential equation. Bessel function jn ode representation (y(x)=j n(x) is a.
(PDF) A differentiation formula for spherical Bessel functions
Integrating the differential relations leads to the integral relations. Let’s begin with a derivative. We begin with a derivation of the bessel functions ja(x) and ya(x), which are two solutions to bessel's di erential equation. There are numerous identities involving bessel functions which may now be generated using the above definitions. Bessel function jn ode representation (y(x)=j n(x) is a.
integration product of bessel function integral Mathematics Stack
We begin with a derivation of the bessel functions ja(x) and ya(x), which are two solutions to bessel's di erential equation. There are numerous identities involving bessel functions which may now be generated using the above definitions. Integrating the differential relations leads to the integral relations. Let’s begin with a derivative. Bessel function jn ode representation (y(x)=j n(x) is a.
Generating Function For Bessel Function
There are numerous identities involving bessel functions which may now be generated using the above definitions. We begin with a derivation of the bessel functions ja(x) and ya(x), which are two solutions to bessel's di erential equation. Let’s begin with a derivative. Bessel function jn ode representation (y(x)=j n(x) is a solution to this ode) x2y xx +xy x +(x.
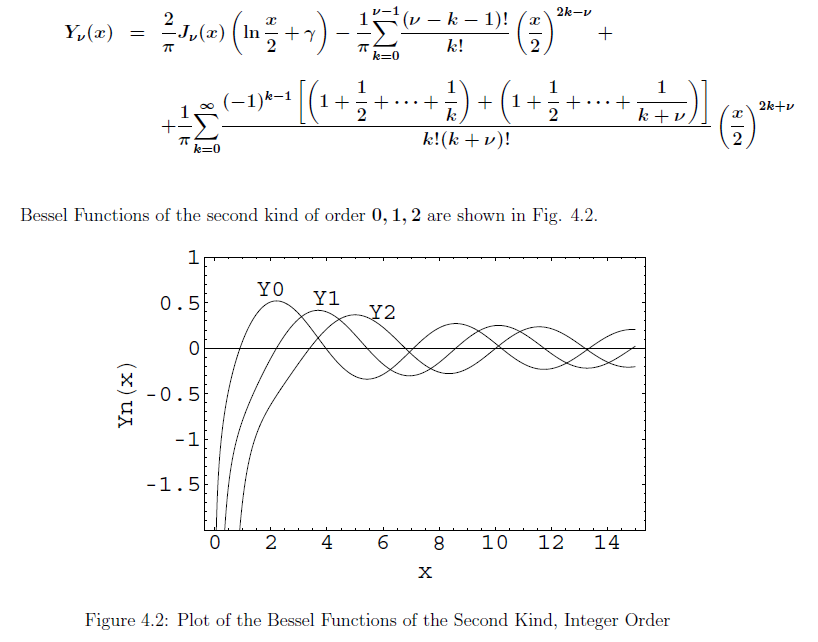
Bessel Function Jn Ode Representation (Y(X)=J N(X) Is A Solution To This Ode) X2Y Xx +Xy X +(X 2 −N2)Y =0 (1) Series.
There are numerous identities involving bessel functions which may now be generated using the above definitions. Let’s begin with a derivative. We begin with a derivation of the bessel functions ja(x) and ya(x), which are two solutions to bessel's di erential equation. Integrating the differential relations leads to the integral relations.