Differentiation Of Delta Function - The crucial difference is that the fourth condition in the definition of the dirac delta ``function'' is replaced by the second condition in the list that. In this paper, dirac delta function is revisited and we derive the nth derivative of dirac delta function and evaluate the fourier transform of. In this section we introduce the dirac delta function and derive the laplace transform of the dirac delta function. $\delta$ thus acts on a test. Now we can define a distribution $\delta$ on a given space of test functions $x$ by $\delta(f)=f(0)$.
In this section we introduce the dirac delta function and derive the laplace transform of the dirac delta function. $\delta$ thus acts on a test. Now we can define a distribution $\delta$ on a given space of test functions $x$ by $\delta(f)=f(0)$. The crucial difference is that the fourth condition in the definition of the dirac delta ``function'' is replaced by the second condition in the list that. In this paper, dirac delta function is revisited and we derive the nth derivative of dirac delta function and evaluate the fourier transform of.
In this section we introduce the dirac delta function and derive the laplace transform of the dirac delta function. The crucial difference is that the fourth condition in the definition of the dirac delta ``function'' is replaced by the second condition in the list that. In this paper, dirac delta function is revisited and we derive the nth derivative of dirac delta function and evaluate the fourier transform of. Now we can define a distribution $\delta$ on a given space of test functions $x$ by $\delta(f)=f(0)$. $\delta$ thus acts on a test.
Mathematical Methods for Physicists, KSU Physics
$\delta$ thus acts on a test. In this section we introduce the dirac delta function and derive the laplace transform of the dirac delta function. In this paper, dirac delta function is revisited and we derive the nth derivative of dirac delta function and evaluate the fourier transform of. The crucial difference is that the fourth condition in the definition.
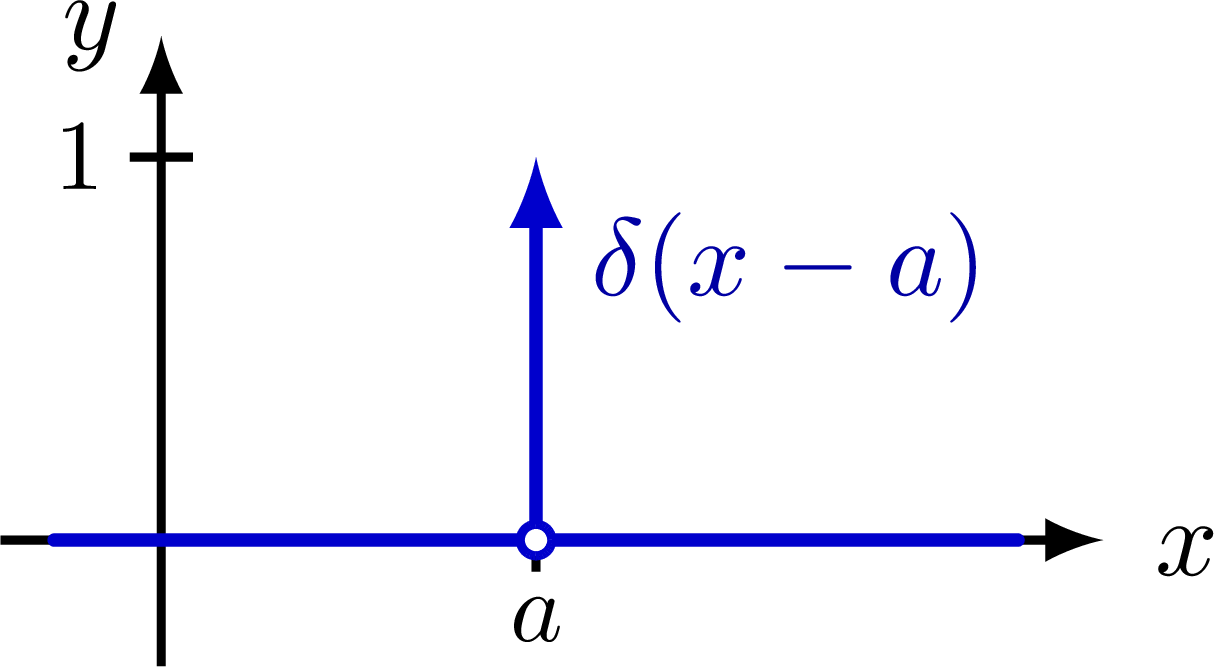
Delta function
Now we can define a distribution $\delta$ on a given space of test functions $x$ by $\delta(f)=f(0)$. In this section we introduce the dirac delta function and derive the laplace transform of the dirac delta function. $\delta$ thus acts on a test. The crucial difference is that the fourth condition in the definition of the dirac delta ``function'' is replaced.
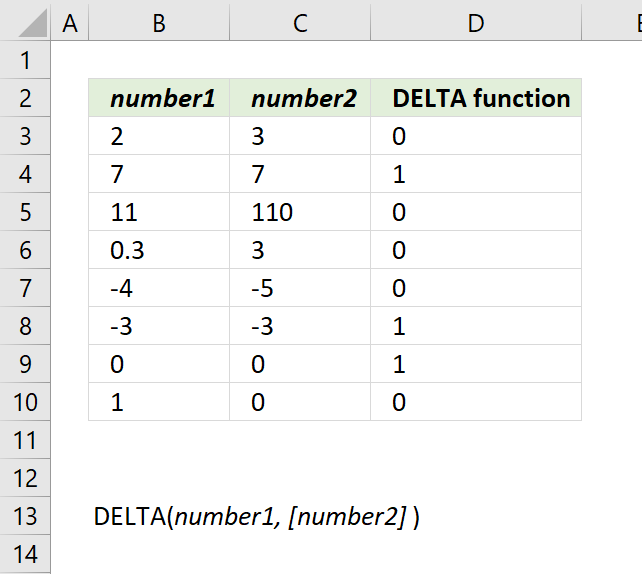
How to use the DELTA function
Now we can define a distribution $\delta$ on a given space of test functions $x$ by $\delta(f)=f(0)$. In this paper, dirac delta function is revisited and we derive the nth derivative of dirac delta function and evaluate the fourier transform of. In this section we introduce the dirac delta function and derive the laplace transform of the dirac delta function..
differentiation Derivative of delta function Physics Stack Exchange
In this paper, dirac delta function is revisited and we derive the nth derivative of dirac delta function and evaluate the fourier transform of. Now we can define a distribution $\delta$ on a given space of test functions $x$ by $\delta(f)=f(0)$. The crucial difference is that the fourth condition in the definition of the dirac delta ``function'' is replaced by.
A Periodic Delta"Function" N 2πi kt PDF Pi Integral
In this paper, dirac delta function is revisited and we derive the nth derivative of dirac delta function and evaluate the fourier transform of. Now we can define a distribution $\delta$ on a given space of test functions $x$ by $\delta(f)=f(0)$. $\delta$ thus acts on a test. In this section we introduce the dirac delta function and derive the laplace.
Mathematical Methods for Physicists, KSU Physics
In this section we introduce the dirac delta function and derive the laplace transform of the dirac delta function. The crucial difference is that the fourth condition in the definition of the dirac delta ``function'' is replaced by the second condition in the list that. $\delta$ thus acts on a test. Now we can define a distribution $\delta$ on a.
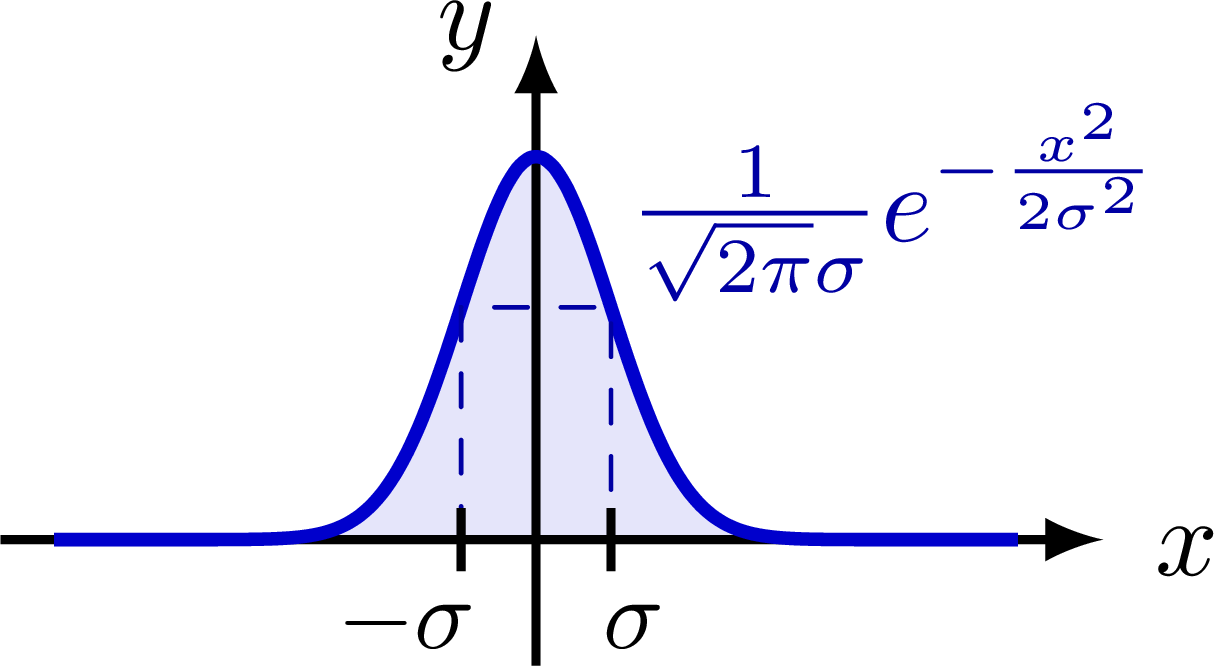
PPT Properties of Delta Function PowerPoint Presentation ID239369
In this paper, dirac delta function is revisited and we derive the nth derivative of dirac delta function and evaluate the fourier transform of. $\delta$ thus acts on a test. In this section we introduce the dirac delta function and derive the laplace transform of the dirac delta function. The crucial difference is that the fourth condition in the definition.
PPT Properties of Delta Function PowerPoint Presentation ID239369
In this section we introduce the dirac delta function and derive the laplace transform of the dirac delta function. In this paper, dirac delta function is revisited and we derive the nth derivative of dirac delta function and evaluate the fourier transform of. The crucial difference is that the fourth condition in the definition of the dirac delta ``function'' is.
Conceptual Tools Impulse Func Def
In this paper, dirac delta function is revisited and we derive the nth derivative of dirac delta function and evaluate the fourier transform of. In this section we introduce the dirac delta function and derive the laplace transform of the dirac delta function. $\delta$ thus acts on a test. The crucial difference is that the fourth condition in the definition.
Delta function
The crucial difference is that the fourth condition in the definition of the dirac delta ``function'' is replaced by the second condition in the list that. $\delta$ thus acts on a test. In this paper, dirac delta function is revisited and we derive the nth derivative of dirac delta function and evaluate the fourier transform of. Now we can define.
$\Delta$ Thus Acts On A Test.
In this section we introduce the dirac delta function and derive the laplace transform of the dirac delta function. In this paper, dirac delta function is revisited and we derive the nth derivative of dirac delta function and evaluate the fourier transform of. The crucial difference is that the fourth condition in the definition of the dirac delta ``function'' is replaced by the second condition in the list that. Now we can define a distribution $\delta$ on a given space of test functions $x$ by $\delta(f)=f(0)$.