Differentiation Of Dot Product - Taking the derivative of this object is just using the. The proof can be extended to any kind of dot product defined. $\map {\mathbf f} x \cdot \dfrac {\map {\d \mathbf f} x} {\d x} =. In fact, recall that for a vector v v, we have that ||v||2 =v ⋅v. You're assuming the dot product is x ∗ y = x0y0 + x1y1 + x2y2 +. | | v | | 2 = v ⋅ v. The dot product of $\mathbf f$ with its derivative is given by:
You're assuming the dot product is x ∗ y = x0y0 + x1y1 + x2y2 +. The dot product of $\mathbf f$ with its derivative is given by: Taking the derivative of this object is just using the. $\map {\mathbf f} x \cdot \dfrac {\map {\d \mathbf f} x} {\d x} =. | | v | | 2 = v ⋅ v. The proof can be extended to any kind of dot product defined. In fact, recall that for a vector v v, we have that ||v||2 =v ⋅v.
Taking the derivative of this object is just using the. | | v | | 2 = v ⋅ v. The proof can be extended to any kind of dot product defined. In fact, recall that for a vector v v, we have that ||v||2 =v ⋅v. $\map {\mathbf f} x \cdot \dfrac {\map {\d \mathbf f} x} {\d x} =. The dot product of $\mathbf f$ with its derivative is given by: You're assuming the dot product is x ∗ y = x0y0 + x1y1 + x2y2 +.
Product Differentiation 101
$\map {\mathbf f} x \cdot \dfrac {\map {\d \mathbf f} x} {\d x} =. In fact, recall that for a vector v v, we have that ||v||2 =v ⋅v. The proof can be extended to any kind of dot product defined. Taking the derivative of this object is just using the. The dot product of $\mathbf f$ with its derivative.
The Comprehensive Guide to Understanding Dot Products The Knowledge Hub
$\map {\mathbf f} x \cdot \dfrac {\map {\d \mathbf f} x} {\d x} =. The proof can be extended to any kind of dot product defined. In fact, recall that for a vector v v, we have that ||v||2 =v ⋅v. You're assuming the dot product is x ∗ y = x0y0 + x1y1 + x2y2 +. The dot product.
Write a Note on Product Differentiation MBA Notesworld
You're assuming the dot product is x ∗ y = x0y0 + x1y1 + x2y2 +. In fact, recall that for a vector v v, we have that ||v||2 =v ⋅v. | | v | | 2 = v ⋅ v. The dot product of $\mathbf f$ with its derivative is given by: $\map {\mathbf f} x \cdot \dfrac {\map.
Dot Product dan cross product PDF
The dot product of $\mathbf f$ with its derivative is given by: You're assuming the dot product is x ∗ y = x0y0 + x1y1 + x2y2 +. | | v | | 2 = v ⋅ v. $\map {\mathbf f} x \cdot \dfrac {\map {\d \mathbf f} x} {\d x} =. In fact, recall that for a vector v.
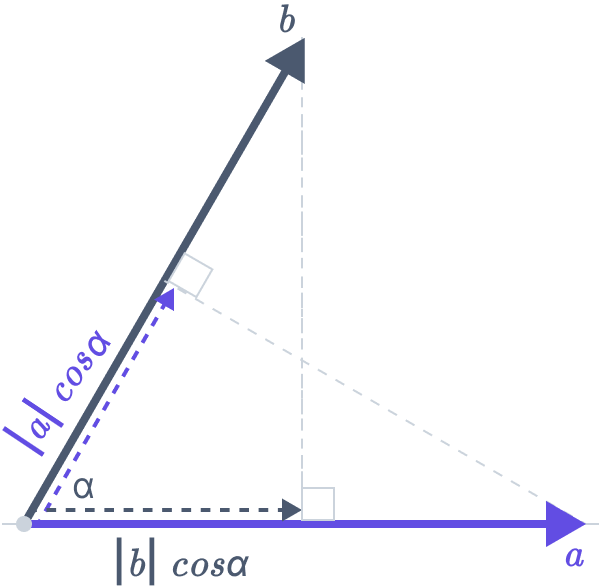
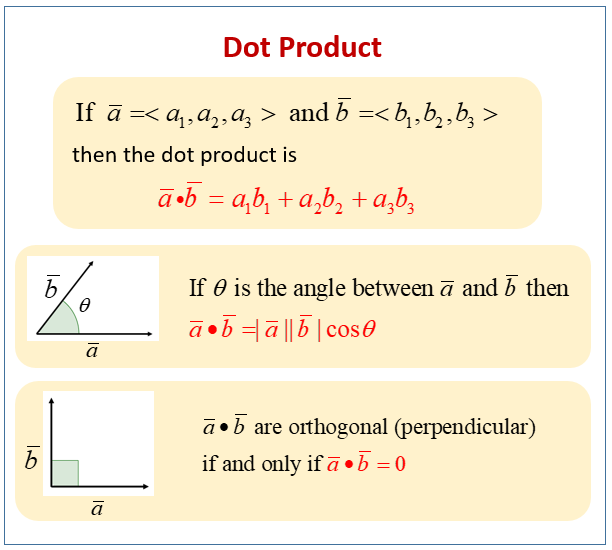
The Dot Product Definition and Example Math lab, Algebra, Mathematics
In fact, recall that for a vector v v, we have that ||v||2 =v ⋅v. The proof can be extended to any kind of dot product defined. | | v | | 2 = v ⋅ v. You're assuming the dot product is x ∗ y = x0y0 + x1y1 + x2y2 +. Taking the derivative of this object is.
Dot Product Calculator The Mathematics Master
In fact, recall that for a vector v v, we have that ||v||2 =v ⋅v. You're assuming the dot product is x ∗ y = x0y0 + x1y1 + x2y2 +. Taking the derivative of this object is just using the. $\map {\mathbf f} x \cdot \dfrac {\map {\d \mathbf f} x} {\d x} =. The proof can be extended.
Product Differentiation Curves
You're assuming the dot product is x ∗ y = x0y0 + x1y1 + x2y2 +. Taking the derivative of this object is just using the. In fact, recall that for a vector v v, we have that ||v||2 =v ⋅v. The dot product of $\mathbf f$ with its derivative is given by: $\map {\mathbf f} x \cdot \dfrac {\map.
The Dot Product (solutions, examples, videos)
In fact, recall that for a vector v v, we have that ||v||2 =v ⋅v. You're assuming the dot product is x ∗ y = x0y0 + x1y1 + x2y2 +. The dot product of $\mathbf f$ with its derivative is given by: The proof can be extended to any kind of dot product defined. | | v | |.
The Comprehensive Guide to Understanding Dot Products The Knowledge Hub
The dot product of $\mathbf f$ with its derivative is given by: You're assuming the dot product is x ∗ y = x0y0 + x1y1 + x2y2 +. In fact, recall that for a vector v v, we have that ||v||2 =v ⋅v. $\map {\mathbf f} x \cdot \dfrac {\map {\d \mathbf f} x} {\d x} =. The proof can.
Dot Product After1995
The proof can be extended to any kind of dot product defined. You're assuming the dot product is x ∗ y = x0y0 + x1y1 + x2y2 +. In fact, recall that for a vector v v, we have that ||v||2 =v ⋅v. | | v | | 2 = v ⋅ v. $\map {\mathbf f} x \cdot \dfrac {\map.
The Proof Can Be Extended To Any Kind Of Dot Product Defined.
In fact, recall that for a vector v v, we have that ||v||2 =v ⋅v. | | v | | 2 = v ⋅ v. Taking the derivative of this object is just using the. You're assuming the dot product is x ∗ y = x0y0 + x1y1 + x2y2 +.
The Dot Product Of $\Mathbf F$ With Its Derivative Is Given By:
$\map {\mathbf f} x \cdot \dfrac {\map {\d \mathbf f} x} {\d x} =.