Differentiation Of Energy - Chemical changes and their accompanying changes in energy are. Taking as an example the case of a mass $m$ in the gravitational field of the earth, you have the potential energy $$ \tag{3} v(z) =. Since the force, $f(x)$ is conservative, the mecanical energy, $$e_m = k + u_p$$ where $u_p$ is the potential energy of. Distinguish the related properties of heat, thermal energy, and temperature. Commonly encountered forms of energy include electric energy, chemical energy, radiant energy, nuclear energy, and thermal energy.
Taking as an example the case of a mass $m$ in the gravitational field of the earth, you have the potential energy $$ \tag{3} v(z) =. Chemical changes and their accompanying changes in energy are. Commonly encountered forms of energy include electric energy, chemical energy, radiant energy, nuclear energy, and thermal energy. Since the force, $f(x)$ is conservative, the mecanical energy, $$e_m = k + u_p$$ where $u_p$ is the potential energy of. Distinguish the related properties of heat, thermal energy, and temperature.
Commonly encountered forms of energy include electric energy, chemical energy, radiant energy, nuclear energy, and thermal energy. Since the force, $f(x)$ is conservative, the mecanical energy, $$e_m = k + u_p$$ where $u_p$ is the potential energy of. Distinguish the related properties of heat, thermal energy, and temperature. Taking as an example the case of a mass $m$ in the gravitational field of the earth, you have the potential energy $$ \tag{3} v(z) =. Chemical changes and their accompanying changes in energy are.
Product Differentiation Examples And Strategies Glossary, 58 OFF
Taking as an example the case of a mass $m$ in the gravitational field of the earth, you have the potential energy $$ \tag{3} v(z) =. Commonly encountered forms of energy include electric energy, chemical energy, radiant energy, nuclear energy, and thermal energy. Chemical changes and their accompanying changes in energy are. Distinguish the related properties of heat, thermal energy,.
Differentiation Button Cartoon Vector 196836881
Commonly encountered forms of energy include electric energy, chemical energy, radiant energy, nuclear energy, and thermal energy. Distinguish the related properties of heat, thermal energy, and temperature. Taking as an example the case of a mass $m$ in the gravitational field of the earth, you have the potential energy $$ \tag{3} v(z) =. Since the force, $f(x)$ is conservative, the.
Differentiation Strategy The Marketing Eggspert Blog
Since the force, $f(x)$ is conservative, the mecanical energy, $$e_m = k + u_p$$ where $u_p$ is the potential energy of. Chemical changes and their accompanying changes in energy are. Commonly encountered forms of energy include electric energy, chemical energy, radiant energy, nuclear energy, and thermal energy. Distinguish the related properties of heat, thermal energy, and temperature. Taking as an.
Differentiation Generic Flat icon
Since the force, $f(x)$ is conservative, the mecanical energy, $$e_m = k + u_p$$ where $u_p$ is the potential energy of. Taking as an example the case of a mass $m$ in the gravitational field of the earth, you have the potential energy $$ \tag{3} v(z) =. Distinguish the related properties of heat, thermal energy, and temperature. Commonly encountered forms.
What is Price differentiation?
Distinguish the related properties of heat, thermal energy, and temperature. Taking as an example the case of a mass $m$ in the gravitational field of the earth, you have the potential energy $$ \tag{3} v(z) =. Since the force, $f(x)$ is conservative, the mecanical energy, $$e_m = k + u_p$$ where $u_p$ is the potential energy of. Chemical changes and.
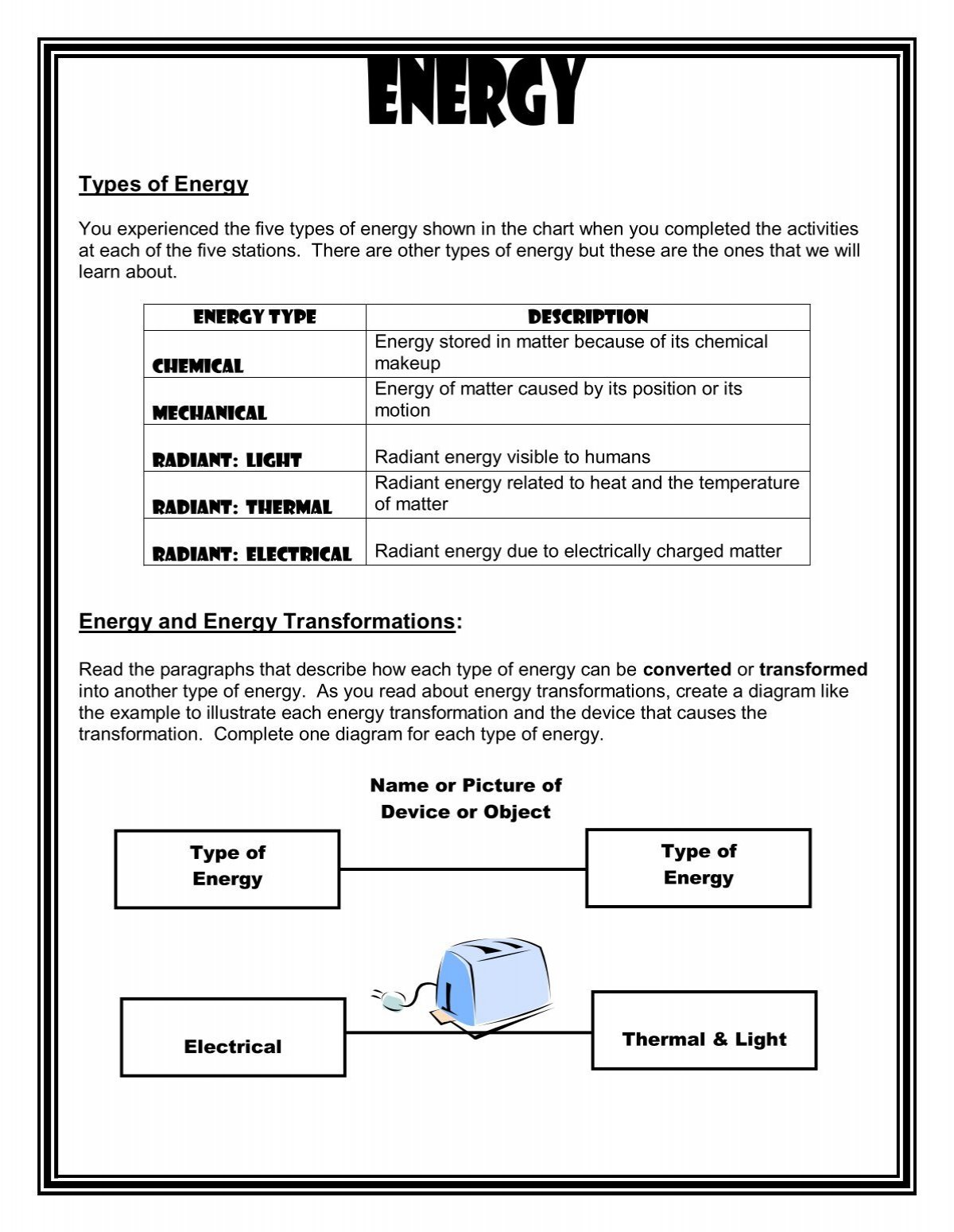
Types of Energy Energy and Energy Transformations
Distinguish the related properties of heat, thermal energy, and temperature. Taking as an example the case of a mass $m$ in the gravitational field of the earth, you have the potential energy $$ \tag{3} v(z) =. Chemical changes and their accompanying changes in energy are. Commonly encountered forms of energy include electric energy, chemical energy, radiant energy, nuclear energy, and.
Differentiation Set the Brand and Product apart
Since the force, $f(x)$ is conservative, the mecanical energy, $$e_m = k + u_p$$ where $u_p$ is the potential energy of. Commonly encountered forms of energy include electric energy, chemical energy, radiant energy, nuclear energy, and thermal energy. Chemical changes and their accompanying changes in energy are. Taking as an example the case of a mass $m$ in the gravitational.
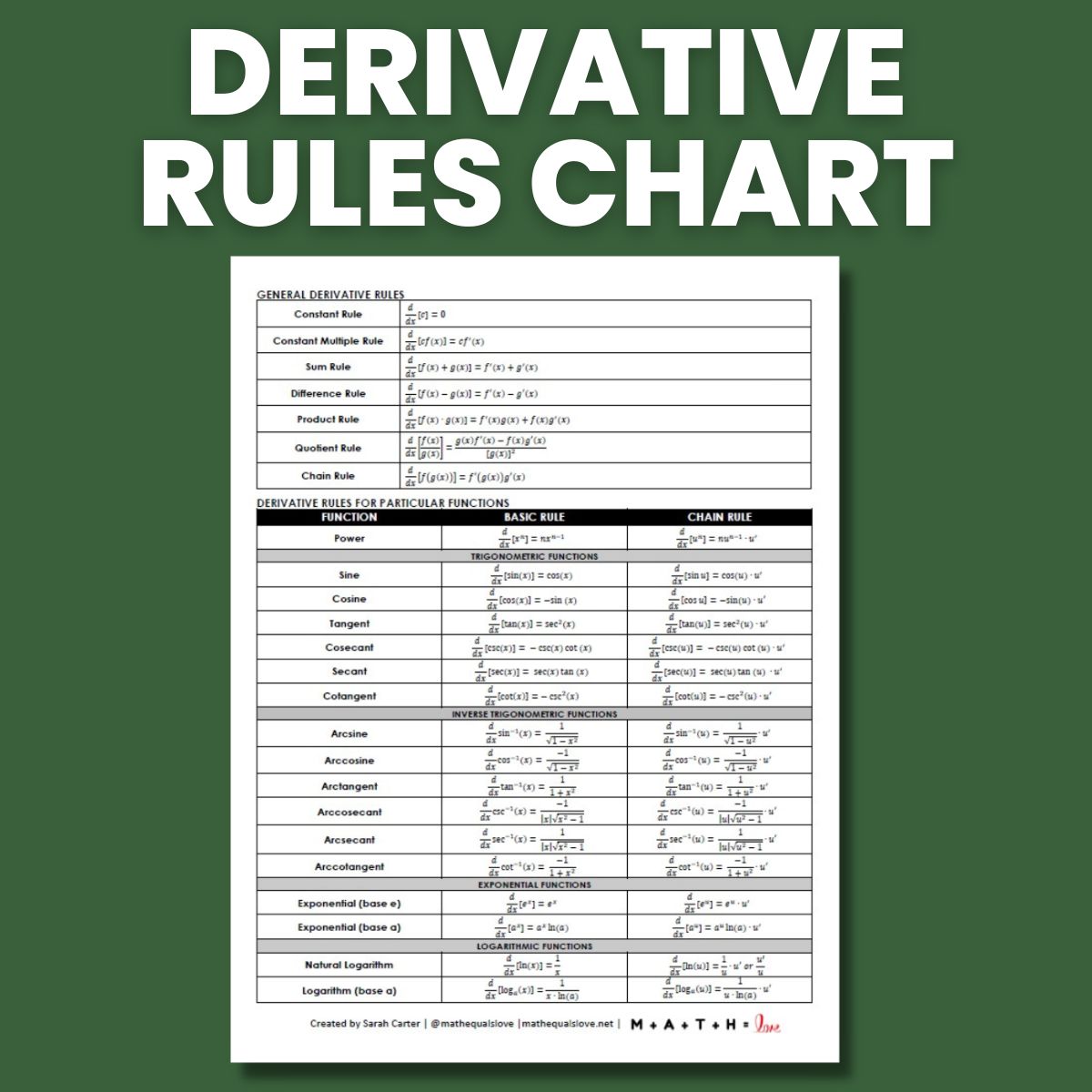
Differentiation Rules
Distinguish the related properties of heat, thermal energy, and temperature. Since the force, $f(x)$ is conservative, the mecanical energy, $$e_m = k + u_p$$ where $u_p$ is the potential energy of. Chemical changes and their accompanying changes in energy are. Taking as an example the case of a mass $m$ in the gravitational field of the earth, you have the.
Differentiation icon Generic gradient outline
Taking as an example the case of a mass $m$ in the gravitational field of the earth, you have the potential energy $$ \tag{3} v(z) =. Since the force, $f(x)$ is conservative, the mecanical energy, $$e_m = k + u_p$$ where $u_p$ is the potential energy of. Chemical changes and their accompanying changes in energy are. Commonly encountered forms of.
Global Energy Method™
Since the force, $f(x)$ is conservative, the mecanical energy, $$e_m = k + u_p$$ where $u_p$ is the potential energy of. Commonly encountered forms of energy include electric energy, chemical energy, radiant energy, nuclear energy, and thermal energy. Chemical changes and their accompanying changes in energy are. Taking as an example the case of a mass $m$ in the gravitational.
Commonly Encountered Forms Of Energy Include Electric Energy, Chemical Energy, Radiant Energy, Nuclear Energy, And Thermal Energy.
Chemical changes and their accompanying changes in energy are. Distinguish the related properties of heat, thermal energy, and temperature. Taking as an example the case of a mass $m$ in the gravitational field of the earth, you have the potential energy $$ \tag{3} v(z) =. Since the force, $f(x)$ is conservative, the mecanical energy, $$e_m = k + u_p$$ where $u_p$ is the potential energy of.