Differentiation Of Force - In a scenario where you consider a. Force is the time derivative of momentum: F = dp dt ⇔ dp =f dt f = d p → d t ⇔ d p = f d t. For our purposes, the differential refers to “an infinitesimally small amount of time.” the differential refers to the corresponding. In my lecture today my professor briefly mentioned that force is the derivative of energy but i did not really get what he meant by. Why is the force being the differential of a potential equivalent to it being a conservative force?
F = dp dt ⇔ dp =f dt f = d p → d t ⇔ d p = f d t. Force is the time derivative of momentum: In my lecture today my professor briefly mentioned that force is the derivative of energy but i did not really get what he meant by. In a scenario where you consider a. Why is the force being the differential of a potential equivalent to it being a conservative force? For our purposes, the differential refers to “an infinitesimally small amount of time.” the differential refers to the corresponding.
In my lecture today my professor briefly mentioned that force is the derivative of energy but i did not really get what he meant by. In a scenario where you consider a. Why is the force being the differential of a potential equivalent to it being a conservative force? F = dp dt ⇔ dp =f dt f = d p → d t ⇔ d p = f d t. For our purposes, the differential refers to “an infinitesimally small amount of time.” the differential refers to the corresponding. Force is the time derivative of momentum:
Differentiation An Important Marketing Strategy Technique Career Parts
For our purposes, the differential refers to “an infinitesimally small amount of time.” the differential refers to the corresponding. Why is the force being the differential of a potential equivalent to it being a conservative force? In a scenario where you consider a. F = dp dt ⇔ dp =f dt f = d p → d t ⇔ d.
Product Differentiation How to Strategize for Business Success ClickUp
In my lecture today my professor briefly mentioned that force is the derivative of energy but i did not really get what he meant by. In a scenario where you consider a. Force is the time derivative of momentum: For our purposes, the differential refers to “an infinitesimally small amount of time.” the differential refers to the corresponding. Why is.
Differentiation Button Cartoon Vector 196836881
Force is the time derivative of momentum: Why is the force being the differential of a potential equivalent to it being a conservative force? In my lecture today my professor briefly mentioned that force is the derivative of energy but i did not really get what he meant by. For our purposes, the differential refers to “an infinitesimally small amount.
Product Differentiation Examples And Strategies Glossary, 58 OFF
For our purposes, the differential refers to “an infinitesimally small amount of time.” the differential refers to the corresponding. F = dp dt ⇔ dp =f dt f = d p → d t ⇔ d p = f d t. In a scenario where you consider a. Force is the time derivative of momentum: In my lecture today my.
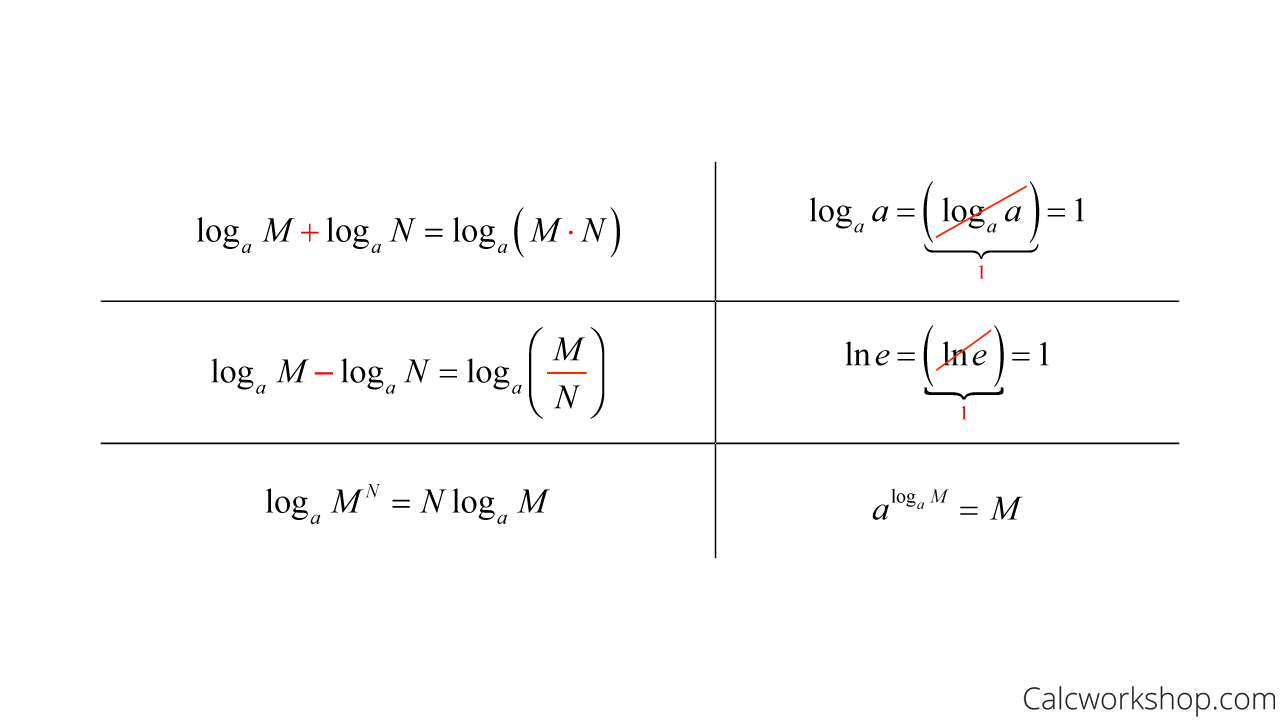
Logarithmic Differentiation (w/ 7 StepbyStep Examples!)
F = dp dt ⇔ dp =f dt f = d p → d t ⇔ d p = f d t. Force is the time derivative of momentum: For our purposes, the differential refers to “an infinitesimally small amount of time.” the differential refers to the corresponding. In my lecture today my professor briefly mentioned that force is the.
Differentiation doesn’t matter, distinctiveness does
In my lecture today my professor briefly mentioned that force is the derivative of energy but i did not really get what he meant by. In a scenario where you consider a. Force is the time derivative of momentum: Why is the force being the differential of a potential equivalent to it being a conservative force? For our purposes, the.
force = mass × acceleration =2.5×12=30 N WH. BASED ON DIFFERENTIATION 1.
F = dp dt ⇔ dp =f dt f = d p → d t ⇔ d p = f d t. In a scenario where you consider a. In my lecture today my professor briefly mentioned that force is the derivative of energy but i did not really get what he meant by. Why is the force being the.
Differentiation Formulas Toppers Bulletin
In a scenario where you consider a. In my lecture today my professor briefly mentioned that force is the derivative of energy but i did not really get what he meant by. Force is the time derivative of momentum: For our purposes, the differential refers to “an infinitesimally small amount of time.” the differential refers to the corresponding. F =.
Master Template
In my lecture today my professor briefly mentioned that force is the derivative of energy but i did not really get what he meant by. For our purposes, the differential refers to “an infinitesimally small amount of time.” the differential refers to the corresponding. F = dp dt ⇔ dp =f dt f = d p → d t ⇔.
Differentiation From First Principles Gradient Of A Curve
Force is the time derivative of momentum: Why is the force being the differential of a potential equivalent to it being a conservative force? F = dp dt ⇔ dp =f dt f = d p → d t ⇔ d p = f d t. In my lecture today my professor briefly mentioned that force is the derivative of.
Force Is The Time Derivative Of Momentum:
F = dp dt ⇔ dp =f dt f = d p → d t ⇔ d p = f d t. In a scenario where you consider a. For our purposes, the differential refers to “an infinitesimally small amount of time.” the differential refers to the corresponding. Why is the force being the differential of a potential equivalent to it being a conservative force?