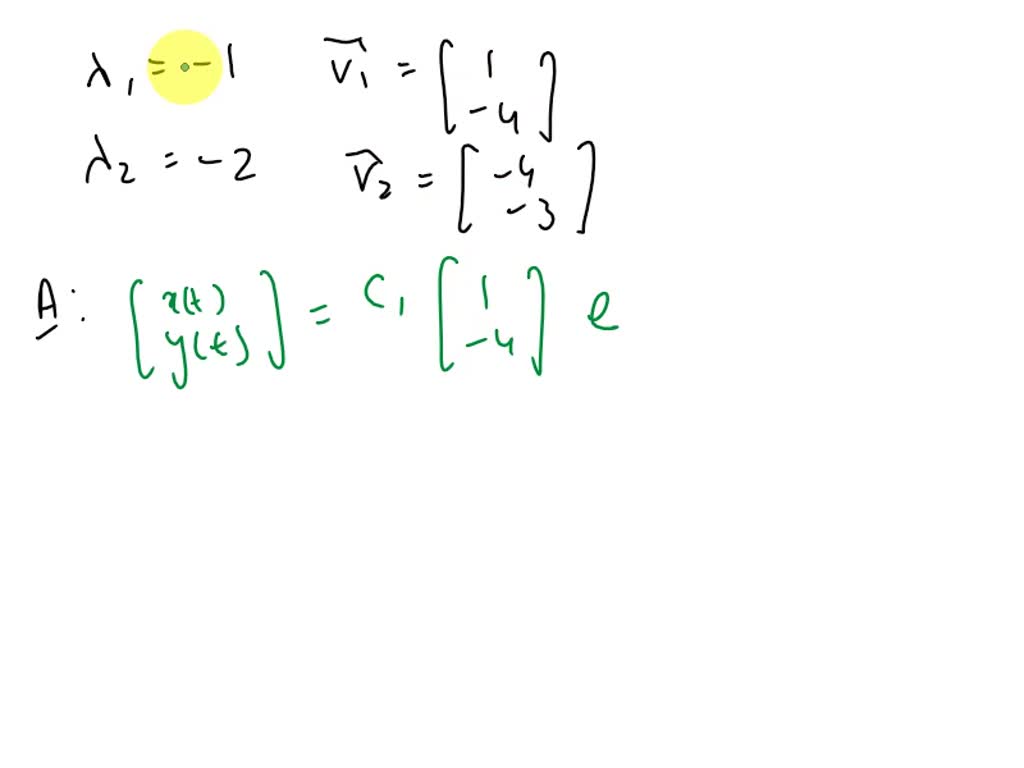Eigenvalue Differential Equations - The pieces of the solution are u(t) = eλtx instead of un =. In this section we will introduce the concept of eigenvalues and eigenvectors of a matrix. We define the characteristic polynomial. Typically, we are given the matrix \(a\) and have to determine the eigenvalues, \(\lambda\), and the associated eigenvectors,. This chapter ends by solving linear differential equations du/dt = au. In this section we will learn how to solve linear homogeneous constant coefficient systems of odes by the eigenvalue method. That is, we want to nd x and such that. Let's nd the eigenvalues and eigenvectors of our matrix from our system of odes. This section introduces eigenvalues and eigenvectors of a matrix, and discusses the role of the eigenvalues in determining the behavior of.
In this section we will introduce the concept of eigenvalues and eigenvectors of a matrix. That is, we want to nd x and such that. The pieces of the solution are u(t) = eλtx instead of un =. Typically, we are given the matrix \(a\) and have to determine the eigenvalues, \(\lambda\), and the associated eigenvectors,. This section introduces eigenvalues and eigenvectors of a matrix, and discusses the role of the eigenvalues in determining the behavior of. We define the characteristic polynomial. In this section we will learn how to solve linear homogeneous constant coefficient systems of odes by the eigenvalue method. Let's nd the eigenvalues and eigenvectors of our matrix from our system of odes. This chapter ends by solving linear differential equations du/dt = au.
That is, we want to nd x and such that. We define the characteristic polynomial. This section introduces eigenvalues and eigenvectors of a matrix, and discusses the role of the eigenvalues in determining the behavior of. Let's nd the eigenvalues and eigenvectors of our matrix from our system of odes. In this section we will learn how to solve linear homogeneous constant coefficient systems of odes by the eigenvalue method. The pieces of the solution are u(t) = eλtx instead of un =. This chapter ends by solving linear differential equations du/dt = au. In this section we will introduce the concept of eigenvalues and eigenvectors of a matrix. Typically, we are given the matrix \(a\) and have to determine the eigenvalues, \(\lambda\), and the associated eigenvectors,.
Solved Apply The Eigenvalue Method To Find The Particular...
This section introduces eigenvalues and eigenvectors of a matrix, and discusses the role of the eigenvalues in determining the behavior of. In this section we will learn how to solve linear homogeneous constant coefficient systems of odes by the eigenvalue method. Let's nd the eigenvalues and eigenvectors of our matrix from our system of odes. That is, we want to.
Solved Solve the given system of differential equations
In this section we will learn how to solve linear homogeneous constant coefficient systems of odes by the eigenvalue method. This chapter ends by solving linear differential equations du/dt = au. Let's nd the eigenvalues and eigenvectors of our matrix from our system of odes. Typically, we are given the matrix \(a\) and have to determine the eigenvalues, \(\lambda\), and.
SOLVED Differential Equations Suppose that the matrix A has the
In this section we will introduce the concept of eigenvalues and eigenvectors of a matrix. The pieces of the solution are u(t) = eλtx instead of un =. We define the characteristic polynomial. That is, we want to nd x and such that. This chapter ends by solving linear differential equations du/dt = au.
PPT Eigenvalues of Ordinary Differential Equations PowerPoint
This section introduces eigenvalues and eigenvectors of a matrix, and discusses the role of the eigenvalues in determining the behavior of. In this section we will learn how to solve linear homogeneous constant coefficient systems of odes by the eigenvalue method. That is, we want to nd x and such that. The pieces of the solution are u(t) = eλtx.
Eigenvalue Equations
In this section we will introduce the concept of eigenvalues and eigenvectors of a matrix. The pieces of the solution are u(t) = eλtx instead of un =. We define the characteristic polynomial. This chapter ends by solving linear differential equations du/dt = au. Let's nd the eigenvalues and eigenvectors of our matrix from our system of odes.
Solved for differential equations how does division work
This section introduces eigenvalues and eigenvectors of a matrix, and discusses the role of the eigenvalues in determining the behavior of. That is, we want to nd x and such that. The pieces of the solution are u(t) = eλtx instead of un =. This chapter ends by solving linear differential equations du/dt = au. Let's nd the eigenvalues and.
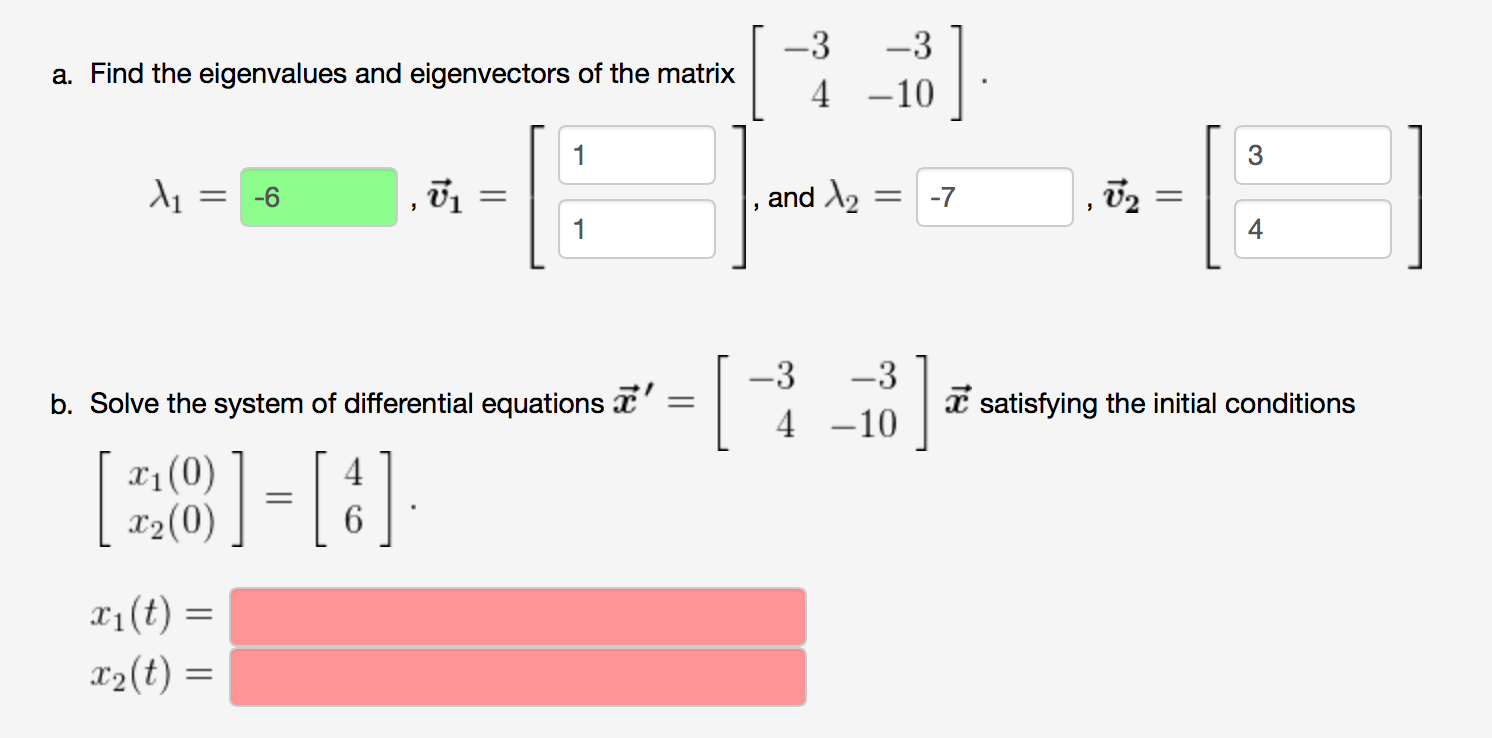
Solved a. Find the eigenvalues and eigenvectors of the
Let's nd the eigenvalues and eigenvectors of our matrix from our system of odes. This chapter ends by solving linear differential equations du/dt = au. We define the characteristic polynomial. In this section we will learn how to solve linear homogeneous constant coefficient systems of odes by the eigenvalue method. The pieces of the solution are u(t) = eλtx instead.
Answered 1. Using the eigenvalue method, solve… bartleby
The pieces of the solution are u(t) = eλtx instead of un =. In this section we will learn how to solve linear homogeneous constant coefficient systems of odes by the eigenvalue method. In this section we will introduce the concept of eigenvalues and eigenvectors of a matrix. This chapter ends by solving linear differential equations du/dt = au. That.
Systems of Differential Equations KZHU.ai 🚀
That is, we want to nd x and such that. In this section we will introduce the concept of eigenvalues and eigenvectors of a matrix. This section introduces eigenvalues and eigenvectors of a matrix, and discusses the role of the eigenvalues in determining the behavior of. Let's nd the eigenvalues and eigenvectors of our matrix from our system of odes..
Systems of Differential Equations KZHU.ai 🚀
We define the characteristic polynomial. This chapter ends by solving linear differential equations du/dt = au. This section introduces eigenvalues and eigenvectors of a matrix, and discusses the role of the eigenvalues in determining the behavior of. Let's nd the eigenvalues and eigenvectors of our matrix from our system of odes. In this section we will introduce the concept of.
Let's Nd The Eigenvalues And Eigenvectors Of Our Matrix From Our System Of Odes.
That is, we want to nd x and such that. This section introduces eigenvalues and eigenvectors of a matrix, and discusses the role of the eigenvalues in determining the behavior of. In this section we will introduce the concept of eigenvalues and eigenvectors of a matrix. In this section we will learn how to solve linear homogeneous constant coefficient systems of odes by the eigenvalue method.
Typically, We Are Given The Matrix \(A\) And Have To Determine The Eigenvalues, \(\Lambda\), And The Associated Eigenvectors,.
This chapter ends by solving linear differential equations du/dt = au. The pieces of the solution are u(t) = eλtx instead of un =. We define the characteristic polynomial.