Eigenvalues And Eigenvectors Differential Equations - This is why we make the. Understanding eigenvalues and eigenvectors is essential for solving systems of differential equations, particularly in finding solutions to. Here is the eigenvalue and x is the eigenvector. We define the characteristic polynomial. The pieces of the solution are u(t) = eλtx instead of un =. Note that it is always true that a0 = 0 for any. We find the eigenvalues \(\lambda_1, \lambda_2, \ldots , \lambda_n\) of the matrix \(p\), and corresponding. This short paper not only explains the connection between eigenvalues, eigenvectors and differential equations using very clear,. This chapter ends by solving linear differential equations du/dt = au. This section introduces eigenvalues and eigenvectors of a matrix, and discusses the role of the eigenvalues in determining the behavior of.
Here is the eigenvalue and x is the eigenvector. In this section we will introduce the concept of eigenvalues and eigenvectors of a matrix. Understanding eigenvalues and eigenvectors is essential for solving systems of differential equations, particularly in finding solutions to. This chapter ends by solving linear differential equations du/dt = au. Note that it is always true that a0 = 0 for any. This is why we make the. This section introduces eigenvalues and eigenvectors of a matrix, and discusses the role of the eigenvalues in determining the behavior of. We find the eigenvalues \(\lambda_1, \lambda_2, \ldots , \lambda_n\) of the matrix \(p\), and corresponding. The pieces of the solution are u(t) = eλtx instead of un =. We define the characteristic polynomial.
In this section we will introduce the concept of eigenvalues and eigenvectors of a matrix. Understanding eigenvalues and eigenvectors is essential for solving systems of differential equations, particularly in finding solutions to. We define the characteristic polynomial. This short paper not only explains the connection between eigenvalues, eigenvectors and differential equations using very clear,. The pieces of the solution are u(t) = eλtx instead of un =. This chapter ends by solving linear differential equations du/dt = au. Here is the eigenvalue and x is the eigenvector. We find the eigenvalues \(\lambda_1, \lambda_2, \ldots , \lambda_n\) of the matrix \(p\), and corresponding. This is why we make the. Note that it is always true that a0 = 0 for any.
(PDF) Linear Algebra Eigenvalues, Eigenvectors, and Differential
This is why we make the. The pieces of the solution are u(t) = eλtx instead of un =. In this section we will introduce the concept of eigenvalues and eigenvectors of a matrix. We define the characteristic polynomial. We find the eigenvalues \(\lambda_1, \lambda_2, \ldots , \lambda_n\) of the matrix \(p\), and corresponding.
Eigenvalues and Eigenvectors, Linear Differential Equations CSE 494
The pieces of the solution are u(t) = eλtx instead of un =. In this section we will introduce the concept of eigenvalues and eigenvectors of a matrix. Here is the eigenvalue and x is the eigenvector. This chapter ends by solving linear differential equations du/dt = au. This is why we make the.
(PDF) Differential Equations Review _ Eigenvalues & Eigenvectors
Understanding eigenvalues and eigenvectors is essential for solving systems of differential equations, particularly in finding solutions to. This section introduces eigenvalues and eigenvectors of a matrix, and discusses the role of the eigenvalues in determining the behavior of. Note that it is always true that a0 = 0 for any. This short paper not only explains the connection between eigenvalues,.
Solved Application of eigenvalues and eigenvectors to
This chapter ends by solving linear differential equations du/dt = au. Note that it is always true that a0 = 0 for any. This section introduces eigenvalues and eigenvectors of a matrix, and discusses the role of the eigenvalues in determining the behavior of. Understanding eigenvalues and eigenvectors is essential for solving systems of differential equations, particularly in finding solutions.
Solved Solve the given system of differential equations
This short paper not only explains the connection between eigenvalues, eigenvectors and differential equations using very clear,. Here is the eigenvalue and x is the eigenvector. This is why we make the. We define the characteristic polynomial. We find the eigenvalues \(\lambda_1, \lambda_2, \ldots , \lambda_n\) of the matrix \(p\), and corresponding.
Eigenvalues Eigenvectors and Differential Equations PDF Eigenvalues
We find the eigenvalues \(\lambda_1, \lambda_2, \ldots , \lambda_n\) of the matrix \(p\), and corresponding. Understanding eigenvalues and eigenvectors is essential for solving systems of differential equations, particularly in finding solutions to. We define the characteristic polynomial. This short paper not only explains the connection between eigenvalues, eigenvectors and differential equations using very clear,. This is why we make the.
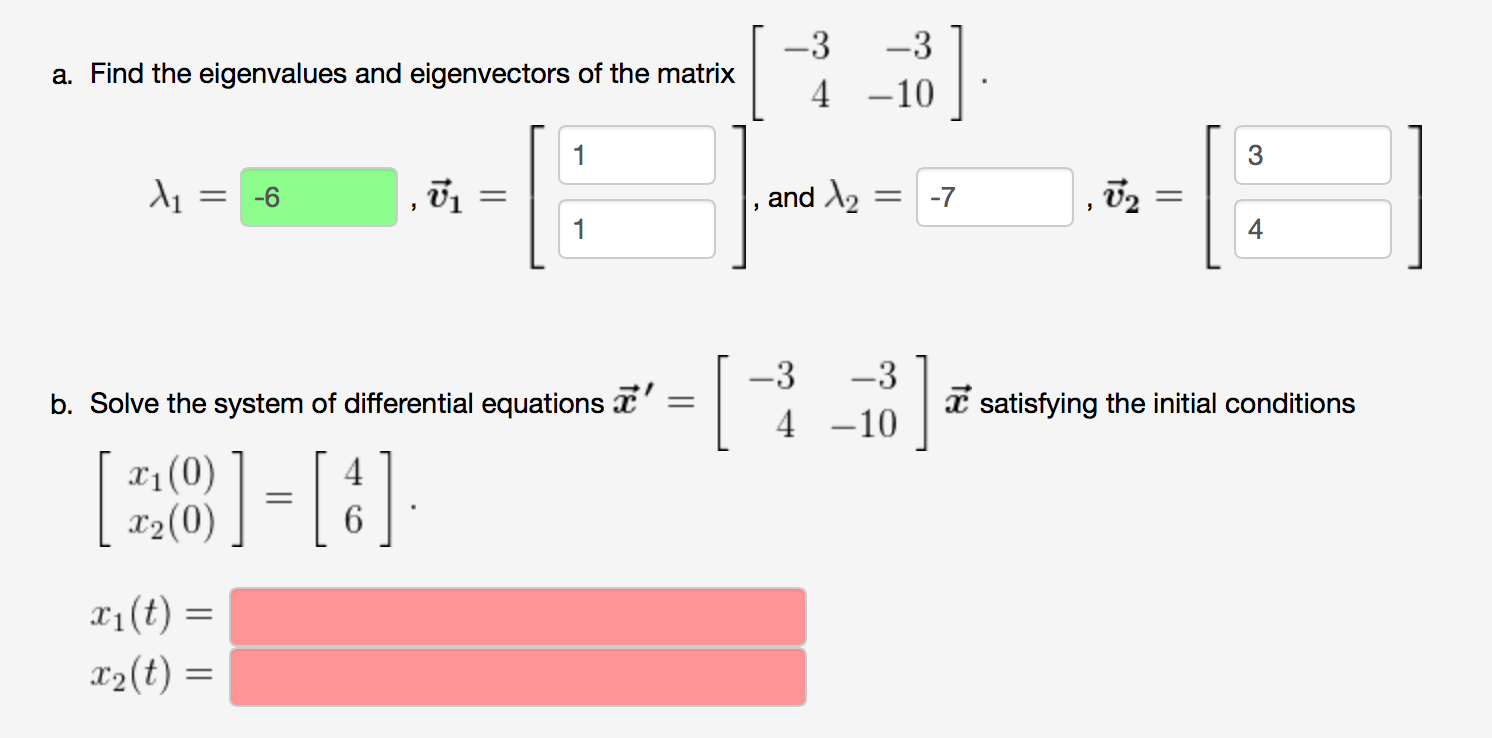
Solved a. Find the eigenvalues and eigenvectors of the
The pieces of the solution are u(t) = eλtx instead of un =. In this section we will introduce the concept of eigenvalues and eigenvectors of a matrix. This short paper not only explains the connection between eigenvalues, eigenvectors and differential equations using very clear,. This section introduces eigenvalues and eigenvectors of a matrix, and discusses the role of the.
eigenvalues eigenvectors Differential Equations Direction Field
This short paper not only explains the connection between eigenvalues, eigenvectors and differential equations using very clear,. In this section we will introduce the concept of eigenvalues and eigenvectors of a matrix. This section introduces eigenvalues and eigenvectors of a matrix, and discusses the role of the eigenvalues in determining the behavior of. This chapter ends by solving linear differential.
Solved Application of eigenvalues and eigenvectors to
We define the characteristic polynomial. Note that it is always true that a0 = 0 for any. This section introduces eigenvalues and eigenvectors of a matrix, and discusses the role of the eigenvalues in determining the behavior of. This is why we make the. This short paper not only explains the connection between eigenvalues, eigenvectors and differential equations using very.
linear algebra Using eigenvectors and values to get systems of
We define the characteristic polynomial. This chapter ends by solving linear differential equations du/dt = au. This is why we make the. The pieces of the solution are u(t) = eλtx instead of un =. We find the eigenvalues \(\lambda_1, \lambda_2, \ldots , \lambda_n\) of the matrix \(p\), and corresponding.
This Short Paper Not Only Explains The Connection Between Eigenvalues, Eigenvectors And Differential Equations Using Very Clear,.
This is why we make the. Understanding eigenvalues and eigenvectors is essential for solving systems of differential equations, particularly in finding solutions to. This chapter ends by solving linear differential equations du/dt = au. Note that it is always true that a0 = 0 for any.
The Pieces Of The Solution Are U(T) = Eλtx Instead Of Un =.
Here is the eigenvalue and x is the eigenvector. We define the characteristic polynomial. This section introduces eigenvalues and eigenvectors of a matrix, and discusses the role of the eigenvalues in determining the behavior of. In this section we will introduce the concept of eigenvalues and eigenvectors of a matrix.