Elliptic Partial Differential Equations - Lu= xn i,j=1 a ij(x)∂ iju(a non. This could model the temperature distribution on a square floor. Elliptic partial differential equations by qing. A course on the method of pseudodifferential operators for elliptic pdes with constant and variable coefficients. Praise for the first edition: Primarily the dirichlet problem for various types of elliptic equations. Differential operator of one of the two forms: A solution to this equation is u(x; Lu= xn i,j=1 ∂ i(a ij(x)∂ ju) (a divergence form operator) 2. Thus, the laplace equation is elliptic.
A course on the method of pseudodifferential operators for elliptic pdes with constant and variable coefficients. Differential operator of one of the two forms: Praise for the first edition: Lu= xn i,j=1 ∂ i(a ij(x)∂ ju) (a divergence form operator) 2. Lu= xn i,j=1 a ij(x)∂ iju(a non. This could model the temperature distribution on a square floor. Elliptic partial differential equations by qing. Thus, the laplace equation is elliptic. Primarily the dirichlet problem for various types of elliptic equations. A solution to this equation is u(x;
Primarily the dirichlet problem for various types of elliptic equations. Thus, the laplace equation is elliptic. This could model the temperature distribution on a square floor. Lu= xn i,j=1 a ij(x)∂ iju(a non. Lu= xn i,j=1 ∂ i(a ij(x)∂ ju) (a divergence form operator) 2. Praise for the first edition: A solution to this equation is u(x; A course on the method of pseudodifferential operators for elliptic pdes with constant and variable coefficients. Elliptic partial differential equations by qing. Differential operator of one of the two forms:
Solved Consider the elliptic partial differential equation
Primarily the dirichlet problem for various types of elliptic equations. Differential operator of one of the two forms: Elliptic partial differential equations by qing. This could model the temperature distribution on a square floor. A course on the method of pseudodifferential operators for elliptic pdes with constant and variable coefficients.
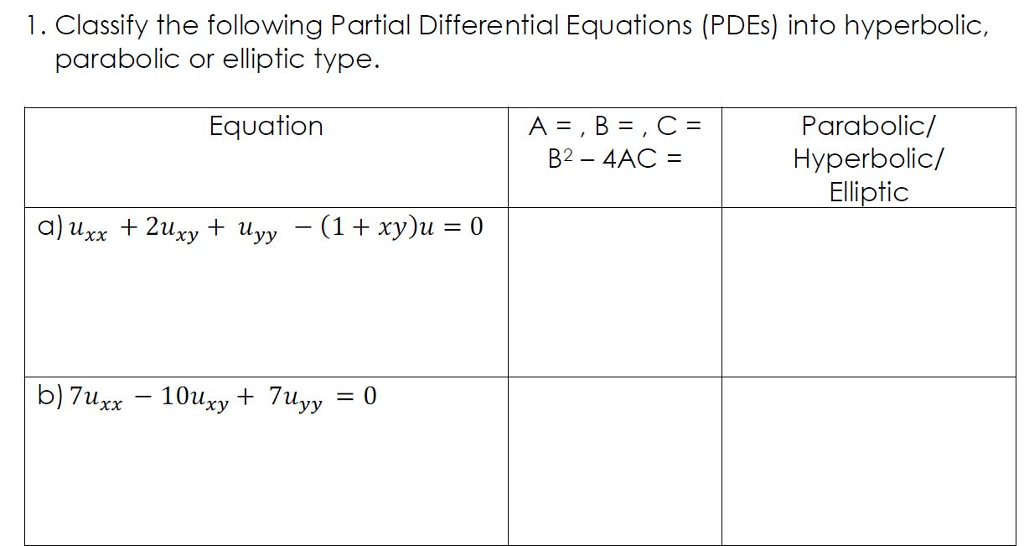
Solved 1. Classify the following Partial Differential
This could model the temperature distribution on a square floor. Differential operator of one of the two forms: Lu= xn i,j=1 ∂ i(a ij(x)∂ ju) (a divergence form operator) 2. Thus, the laplace equation is elliptic. A course on the method of pseudodifferential operators for elliptic pdes with constant and variable coefficients.
(PDF) Elliptic Partial Differential Equations Qualitative
Praise for the first edition: Primarily the dirichlet problem for various types of elliptic equations. This could model the temperature distribution on a square floor. Lu= xn i,j=1 ∂ i(a ij(x)∂ ju) (a divergence form operator) 2. A solution to this equation is u(x;
[Solved] Problem 1. Second order Partial differential equations (PDEs
A course on the method of pseudodifferential operators for elliptic pdes with constant and variable coefficients. Lu= xn i,j=1 a ij(x)∂ iju(a non. Elliptic partial differential equations by qing. Praise for the first edition: Thus, the laplace equation is elliptic.
(PDF) Numerical Solutions of Elliptic Partial Differential Equations by
A course on the method of pseudodifferential operators for elliptic pdes with constant and variable coefficients. Praise for the first edition: Elliptic partial differential equations by qing. A solution to this equation is u(x; This could model the temperature distribution on a square floor.
PPT Elliptic Partial Differential Equations Introduction PowerPoint
A solution to this equation is u(x; Elliptic partial differential equations by qing. Lu= xn i,j=1 ∂ i(a ij(x)∂ ju) (a divergence form operator) 2. Praise for the first edition: This could model the temperature distribution on a square floor.
Solved Solve the elliptic partial differential equation
Lu= xn i,j=1 a ij(x)∂ iju(a non. Lu= xn i,j=1 ∂ i(a ij(x)∂ ju) (a divergence form operator) 2. Differential operator of one of the two forms: Thus, the laplace equation is elliptic. This could model the temperature distribution on a square floor.
Lecture 7_elliptic partial differential equation PDF Equations
Lu= xn i,j=1 a ij(x)∂ iju(a non. A solution to this equation is u(x; Thus, the laplace equation is elliptic. A course on the method of pseudodifferential operators for elliptic pdes with constant and variable coefficients. Praise for the first edition:
PPT PARTIAL DIFFERENTIAL EQUATIONS PowerPoint Presentation ID2511480
A solution to this equation is u(x; A course on the method of pseudodifferential operators for elliptic pdes with constant and variable coefficients. Lu= xn i,j=1 ∂ i(a ij(x)∂ ju) (a divergence form operator) 2. Differential operator of one of the two forms: This could model the temperature distribution on a square floor.
(PDF) The numerical solution of elliptic partial differential equations
A course on the method of pseudodifferential operators for elliptic pdes with constant and variable coefficients. A solution to this equation is u(x; This could model the temperature distribution on a square floor. Primarily the dirichlet problem for various types of elliptic equations. Lu= xn i,j=1 a ij(x)∂ iju(a non.
Differential Operator Of One Of The Two Forms:
Primarily the dirichlet problem for various types of elliptic equations. A solution to this equation is u(x; Thus, the laplace equation is elliptic. Praise for the first edition:
This Could Model The Temperature Distribution On A Square Floor.
A course on the method of pseudodifferential operators for elliptic pdes with constant and variable coefficients. Lu= xn i,j=1 ∂ i(a ij(x)∂ ju) (a divergence form operator) 2. Lu= xn i,j=1 a ij(x)∂ iju(a non. Elliptic partial differential equations by qing.