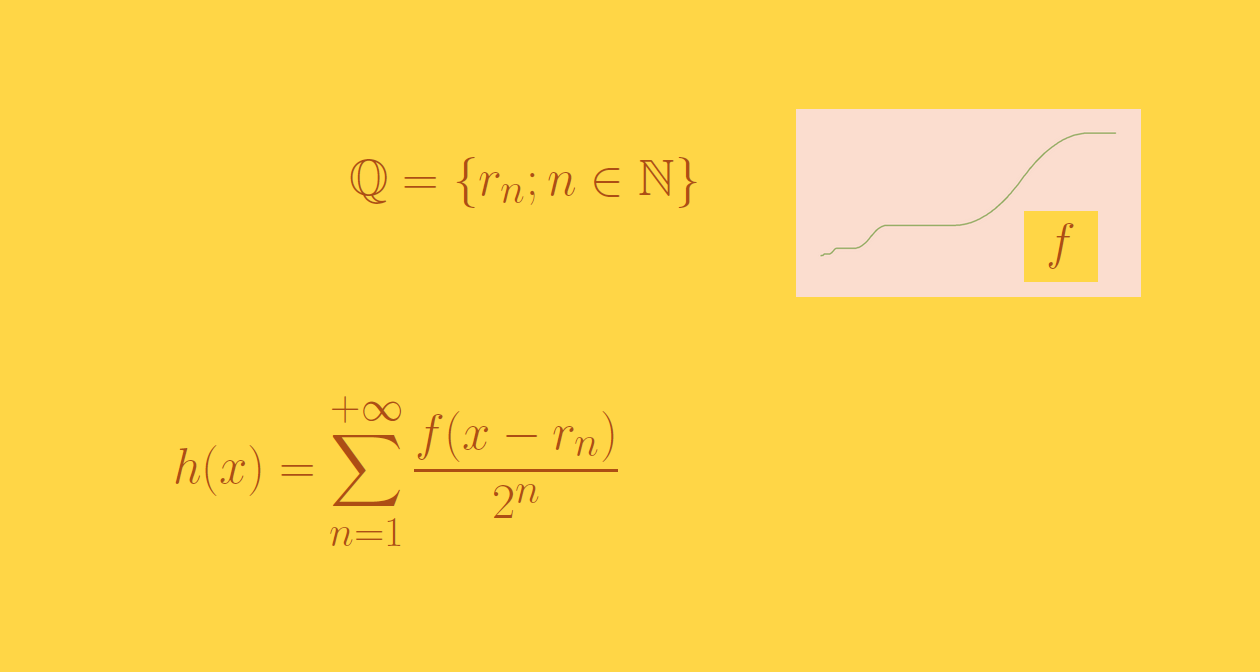Every Continuous Function Is Differentiable True Or False - Let us take an example function which will result into the testing of statement. [a, b] → r be continuously differentiable. So it may seem reasonable that all continuous functions are differentiable a.e. Every continuous function is always differentiable. If a function f (x) is differentiable at a point a, then it is continuous at the point a. The correct option is b false. Show that every differentiable function is continuous (converse is not true i.e., a function may be continuous but not differentiable). But we see that $f(x) = |x|$ is continuous because $\mathop {\lim }\limits_{x \to c} f(x) = \mathop {\lim }\limits_{x \to c} |x| = f(c)$ exists for all. This turns out to be. Then its derivative f′ f ′ is continuous on [a, b] [a, b] and hence.
Show that every differentiable function is continuous (converse is not true i.e., a function may be continuous but not differentiable). [a, b] → r be continuously differentiable. If a function f (x) is differentiable at a point a, then it is continuous at the point a. [a,b]\to {\mathbb r}$ which equals $0$ at $a$, and equals $1$ on the interval $(a,b]$. [a, b] → r f: Every continuous function is always differentiable. But we see that $f(x) = |x|$ is continuous because $\mathop {\lim }\limits_{x \to c} f(x) = \mathop {\lim }\limits_{x \to c} |x| = f(c)$ exists for all. Then its derivative f′ f ′ is continuous on [a, b] [a, b] and hence. So it may seem reasonable that all continuous functions are differentiable a.e. Let us take an example function which will result into the testing of statement.
Then its derivative f′ f ′ is continuous on [a, b] [a, b] and hence. But we see that $f(x) = |x|$ is continuous because $\mathop {\lim }\limits_{x \to c} f(x) = \mathop {\lim }\limits_{x \to c} |x| = f(c)$ exists for all. [a, b] → r f: Every continuous function is always differentiable. Show that every differentiable function is continuous (converse is not true i.e., a function may be continuous but not differentiable). Let us take an example function which will result into the testing of statement. If a function f (x) is differentiable at a point a, then it is continuous at the point a. So it may seem reasonable that all continuous functions are differentiable a.e. [a, b] → r be continuously differentiable. This turns out to be.
Differentiable vs. Continuous Functions Understanding the Distinctions
Then its derivative f′ f ′ is continuous on [a, b] [a, b] and hence. [a, b] → r f: But we see that $f(x) = |x|$ is continuous because $\mathop {\lim }\limits_{x \to c} f(x) = \mathop {\lim }\limits_{x \to c} |x| = f(c)$ exists for all. Every continuous function is always differentiable. [a, b] → r be continuously.
Solved III. 25. Which of the following is/are true? 1. Every
Let us take an example function which will result into the testing of statement. [a, b] → r be continuously differentiable. The correct option is b false. But we see that $f(x) = |x|$ is continuous because $\mathop {\lim }\limits_{x \to c} f(x) = \mathop {\lim }\limits_{x \to c} |x| = f(c)$ exists for all. So it may seem reasonable.
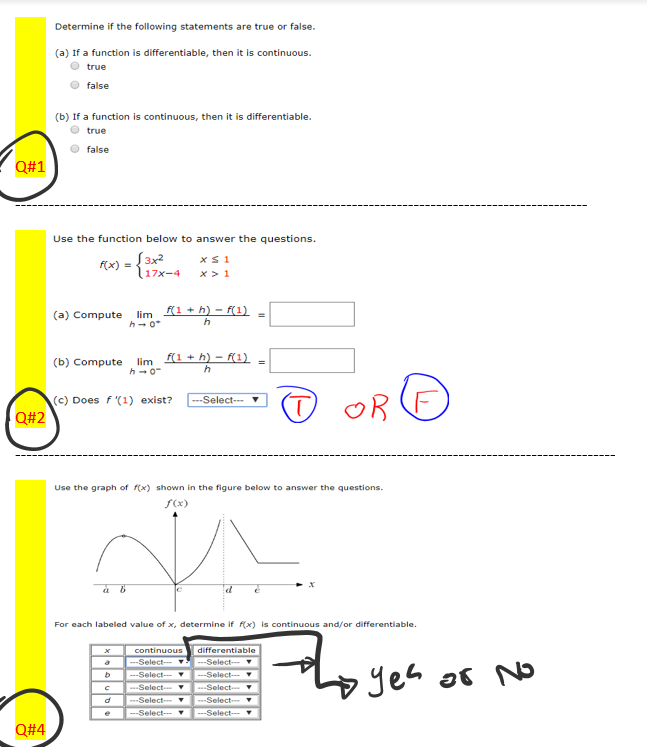
Solved Determine if the following statements are true or
Every continuous function is always differentiable. So it may seem reasonable that all continuous functions are differentiable a.e. The correct option is b false. Then its derivative f′ f ′ is continuous on [a, b] [a, b] and hence. If a function f (x) is differentiable at a point a, then it is continuous at the point a.
SOLVED 'True or False If a function is continuous at point; then it
If a function f (x) is differentiable at a point a, then it is continuous at the point a. But we see that $f(x) = |x|$ is continuous because $\mathop {\lim }\limits_{x \to c} f(x) = \mathop {\lim }\limits_{x \to c} |x| = f(c)$ exists for all. Every continuous function is always differentiable. [a, b] → r f: Let us.
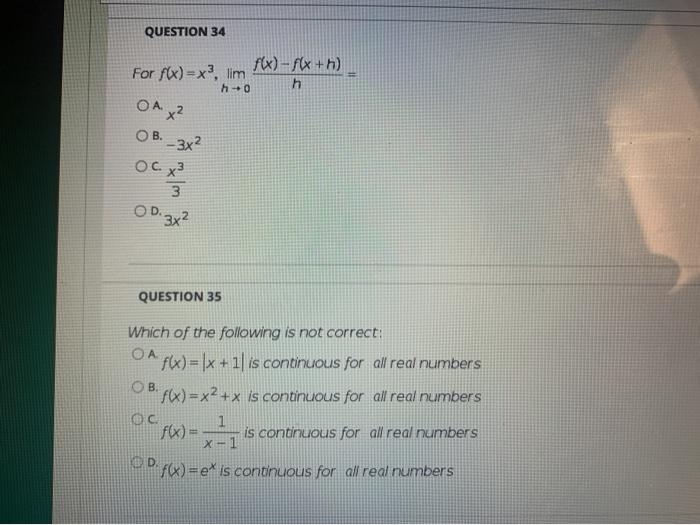
Solved QUESTION 32 Every continuous function is
If a function f (x) is differentiable at a point a, then it is continuous at the point a. The correct option is b false. [a, b] → r be continuously differentiable. Then its derivative f′ f ′ is continuous on [a, b] [a, b] and hence. This turns out to be.
acontinuousfunctionnotdifferentiableontherationals
[a, b] → r f: [a, b] → r be continuously differentiable. So it may seem reasonable that all continuous functions are differentiable a.e. But we see that $f(x) = |x|$ is continuous because $\mathop {\lim }\limits_{x \to c} f(x) = \mathop {\lim }\limits_{x \to c} |x| = f(c)$ exists for all. If a function f (x) is differentiable at.
Solved If f is continuous at a number, x, then f is differentiable at
[a, b] → r be continuously differentiable. If a function f (x) is differentiable at a point a, then it is continuous at the point a. [a, b] → r f: [a,b]\to {\mathbb r}$ which equals $0$ at $a$, and equals $1$ on the interval $(a,b]$. Then its derivative f′ f ′ is continuous on [a, b] [a, b] and.
Solved Among the following statements, which are true and
[a,b]\to {\mathbb r}$ which equals $0$ at $a$, and equals $1$ on the interval $(a,b]$. Show that every differentiable function is continuous (converse is not true i.e., a function may be continuous but not differentiable). But we see that $f(x) = |x|$ is continuous because $\mathop {\lim }\limits_{x \to c} f(x) = \mathop {\lim }\limits_{x \to c} |x| = f(c)$.
Solved 1. True Or False If A Function Is Continuous At A...
[a, b] → r f: So it may seem reasonable that all continuous functions are differentiable a.e. Then its derivative f′ f ′ is continuous on [a, b] [a, b] and hence. Every continuous function is always differentiable. If a function f (x) is differentiable at a point a, then it is continuous at the point a.
VIDEO solution If a function of f is differentiable at x=a then the
If a function f (x) is differentiable at a point a, then it is continuous at the point a. Every continuous function is always differentiable. Let us take an example function which will result into the testing of statement. Then its derivative f′ f ′ is continuous on [a, b] [a, b] and hence. [a, b] → r be continuously.
Every Continuous Function Is Always Differentiable.
The correct option is b false. So it may seem reasonable that all continuous functions are differentiable a.e. Then its derivative f′ f ′ is continuous on [a, b] [a, b] and hence. [a, b] → r f:
Show That Every Differentiable Function Is Continuous (Converse Is Not True I.e., A Function May Be Continuous But Not Differentiable).
[a, b] → r be continuously differentiable. If a function f (x) is differentiable at a point a, then it is continuous at the point a. Let us take an example function which will result into the testing of statement. [a,b]\to {\mathbb r}$ which equals $0$ at $a$, and equals $1$ on the interval $(a,b]$.
This Turns Out To Be.
But we see that $f(x) = |x|$ is continuous because $\mathop {\lim }\limits_{x \to c} f(x) = \mathop {\lim }\limits_{x \to c} |x| = f(c)$ exists for all.