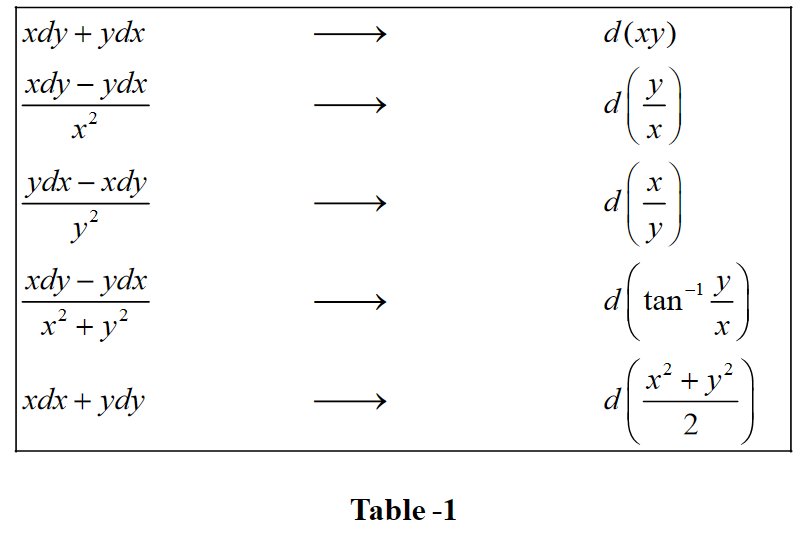
Exact Differential Equations - From the previous example, a potential function for the differential. Is said to be exact. This means that a function u(x,y) exists such that:. P(x,y)dx+q(x,y)dy = 0 if ∂p ∂y = ∂q ∂x then the o.de. This is why such a differential equation is called an exact differential equation. If you have had vector calculus , this is the same as finding the potential functions. A differential equation with a potential function is called exact.
P(x,y)dx+q(x,y)dy = 0 if ∂p ∂y = ∂q ∂x then the o.de. If you have had vector calculus , this is the same as finding the potential functions. This is why such a differential equation is called an exact differential equation. A differential equation with a potential function is called exact. From the previous example, a potential function for the differential. This means that a function u(x,y) exists such that:. Is said to be exact.
Is said to be exact. P(x,y)dx+q(x,y)dy = 0 if ∂p ∂y = ∂q ∂x then the o.de. This means that a function u(x,y) exists such that:. If you have had vector calculus , this is the same as finding the potential functions. A differential equation with a potential function is called exact. This is why such a differential equation is called an exact differential equation. From the previous example, a potential function for the differential.
Examples On Exact Differential Equations What is Examples On Exact
From the previous example, a potential function for the differential. P(x,y)dx+q(x,y)dy = 0 if ∂p ∂y = ∂q ∂x then the o.de. This is why such a differential equation is called an exact differential equation. This means that a function u(x,y) exists such that:. If you have had vector calculus , this is the same as finding the potential functions.
[Solved] SOLVE THE FOLLOWING EXACT DIFFERENTIAL EQUATIONS SOLVE THE
Is said to be exact. This means that a function u(x,y) exists such that:. P(x,y)dx+q(x,y)dy = 0 if ∂p ∂y = ∂q ∂x then the o.de. If you have had vector calculus , this is the same as finding the potential functions. From the previous example, a potential function for the differential.
[Solved] Determine Whether The Following Differential Equations Are
This means that a function u(x,y) exists such that:. Is said to be exact. From the previous example, a potential function for the differential. This is why such a differential equation is called an exact differential equation. A differential equation with a potential function is called exact.
Exact Differential Equations PDF Differential Equations Equations
A differential equation with a potential function is called exact. P(x,y)dx+q(x,y)dy = 0 if ∂p ∂y = ∂q ∂x then the o.de. This means that a function u(x,y) exists such that:. From the previous example, a potential function for the differential. Is said to be exact.
Exact differential equations Yawin
A differential equation with a potential function is called exact. If you have had vector calculus , this is the same as finding the potential functions. This means that a function u(x,y) exists such that:. From the previous example, a potential function for the differential. Is said to be exact.
Differential Equations Owlcation
Is said to be exact. From the previous example, a potential function for the differential. If you have had vector calculus , this is the same as finding the potential functions. This is why such a differential equation is called an exact differential equation. This means that a function u(x,y) exists such that:.
Exact differential equations
P(x,y)dx+q(x,y)dy = 0 if ∂p ∂y = ∂q ∂x then the o.de. If you have had vector calculus , this is the same as finding the potential functions. This means that a function u(x,y) exists such that:. Is said to be exact. A differential equation with a potential function is called exact.
LECTURE 5 Exact Differential Equations PDF Equations Fair Use
P(x,y)dx+q(x,y)dy = 0 if ∂p ∂y = ∂q ∂x then the o.de. This is why such a differential equation is called an exact differential equation. A differential equation with a potential function is called exact. From the previous example, a potential function for the differential. This means that a function u(x,y) exists such that:.
[Solved] SOLVE THE FOLLOWING EXACT DIFFERENTIAL EQUATIONS SOLVE THE
This means that a function u(x,y) exists such that:. This is why such a differential equation is called an exact differential equation. Is said to be exact. A differential equation with a potential function is called exact. From the previous example, a potential function for the differential.
Exact Differential Equations Differential Equations Equations
If you have had vector calculus , this is the same as finding the potential functions. From the previous example, a potential function for the differential. P(x,y)dx+q(x,y)dy = 0 if ∂p ∂y = ∂q ∂x then the o.de. Is said to be exact. A differential equation with a potential function is called exact.
Is Said To Be Exact.
P(x,y)dx+q(x,y)dy = 0 if ∂p ∂y = ∂q ∂x then the o.de. This is why such a differential equation is called an exact differential equation. From the previous example, a potential function for the differential. A differential equation with a potential function is called exact.
This Means That A Function U(X,Y) Exists Such That:.
If you have had vector calculus , this is the same as finding the potential functions.