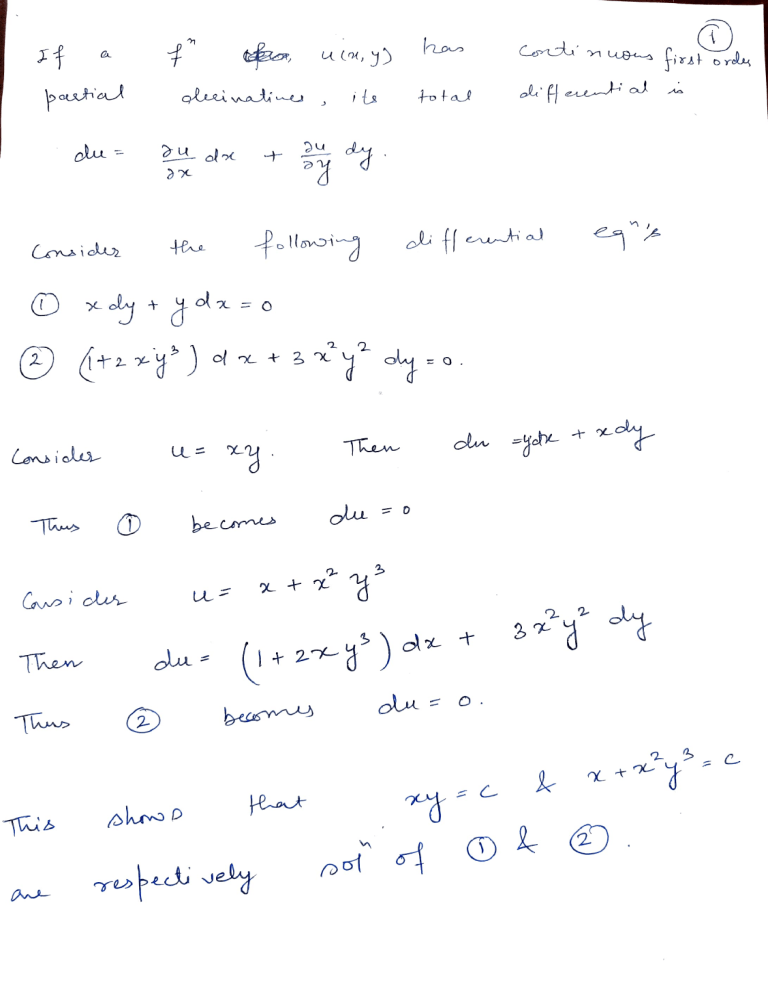Exact Equation Differential Equation

Exact Equation Differential Equation - This means that a function u(x,y) exists such that:. In this article, we are going to discuss what is an exact differential equation, standard form, integrating factor, and how to solve exact. A differential equation with a potential function is called exact. This is why such a differential equation is called an exact differential equation. Is said to be exact. From the previous example, a potential function for the differential. If you have had vector calculus , this is the same as finding the potential functions. P(x,y)dx+q(x,y)dy = 0 if ∂p ∂y = ∂q ∂x then the o.de.

In this article, we are going to discuss what is an exact differential equation, standard form, integrating factor, and how to solve exact. P(x,y)dx+q(x,y)dy = 0 if ∂p ∂y = ∂q ∂x then the o.de. A differential equation with a potential function is called exact. This means that a function u(x,y) exists such that:. This is why such a differential equation is called an exact differential equation. If you have had vector calculus , this is the same as finding the potential functions. From the previous example, a potential function for the differential. Is said to be exact.

A differential equation with a potential function is called exact. This is why such a differential equation is called an exact differential equation. Is said to be exact. This means that a function u(x,y) exists such that:. P(x,y)dx+q(x,y)dy = 0 if ∂p ∂y = ∂q ∂x then the o.de. In this article, we are going to discuss what is an exact differential equation, standard form, integrating factor, and how to solve exact. If you have had vector calculus , this is the same as finding the potential functions. From the previous example, a potential function for the differential.

SOLUTION Differential equations practice problems non exact

A differential equation with a potential function is called exact. This means that a function u(x,y) exists such that:. P(x,y)dx+q(x,y)dy = 0 if ∂p ∂y = ∂q ∂x then the o.de. This is why such a differential equation is called an exact differential equation. In this article, we are going to discuss what is an exact differential equation, standard form,.

Solved Exact Differential Equations Verify that the given

Is said to be exact. This means that a function u(x,y) exists such that:. P(x,y)dx+q(x,y)dy = 0 if ∂p ∂y = ∂q ∂x then the o.de. A differential equation with a potential function is called exact. This is why such a differential equation is called an exact differential equation.

Exact differential equation Alchetron, the free social encyclopedia

From the previous example, a potential function for the differential. This means that a function u(x,y) exists such that:. P(x,y)dx+q(x,y)dy = 0 if ∂p ∂y = ∂q ∂x then the o.de. This is why such a differential equation is called an exact differential equation. Is said to be exact.

SOLUTION Exact equation method 1 example 2 differential equation

From the previous example, a potential function for the differential. This means that a function u(x,y) exists such that:. This is why such a differential equation is called an exact differential equation. If you have had vector calculus , this is the same as finding the potential functions. A differential equation with a potential function is called exact.

exact differential equation

P(x,y)dx+q(x,y)dy = 0 if ∂p ∂y = ∂q ∂x then the o.de. A differential equation with a potential function is called exact. Is said to be exact. This means that a function u(x,y) exists such that:. From the previous example, a potential function for the differential.

Solved Determine whether the given differential equation is

Is said to be exact. From the previous example, a potential function for the differential. In this article, we are going to discuss what is an exact differential equation, standard form, integrating factor, and how to solve exact. This means that a function u(x,y) exists such that:. P(x,y)dx+q(x,y)dy = 0 if ∂p ∂y = ∂q ∂x then the o.de.

[Solved] . Determine whether the given differential equation is exact

Is said to be exact. A differential equation with a potential function is called exact. This is why such a differential equation is called an exact differential equation. This means that a function u(x,y) exists such that:. If you have had vector calculus , this is the same as finding the potential functions.

Engineering Mathematics Reducible to Exact Differential equation

In this article, we are going to discuss what is an exact differential equation, standard form, integrating factor, and how to solve exact. Is said to be exact. From the previous example, a potential function for the differential. This is why such a differential equation is called an exact differential equation. A differential equation with a potential function is called.

[Solved] . Determine whether the given differential equation is exact

P(x,y)dx+q(x,y)dy = 0 if ∂p ∂y = ∂q ∂x then the o.de. In this article, we are going to discuss what is an exact differential equation, standard form, integrating factor, and how to solve exact. If you have had vector calculus , this is the same as finding the potential functions. This means that a function u(x,y) exists such that:..

Exact Differential Equation Definition, Condition with Examples

If you have had vector calculus , this is the same as finding the potential functions. From the previous example, a potential function for the differential. P(x,y)dx+q(x,y)dy = 0 if ∂p ∂y = ∂q ∂x then the o.de. In this article, we are going to discuss what is an exact differential equation, standard form, integrating factor, and how to solve.

This Means That A Function U(X,Y) Exists Such That:.

P(x,y)dx+q(x,y)dy = 0 if ∂p ∂y = ∂q ∂x then the o.de. From the previous example, a potential function for the differential. In this article, we are going to discuss what is an exact differential equation, standard form, integrating factor, and how to solve exact. A differential equation with a potential function is called exact.