Find Differential Dy - Type in any function derivative to get the solution, steps and graph. There is a nice application to differentials. Example 2 find the differential `dy` of the. To find the differential `dy`, we just need to find the derivative and write it with `dx` on the right. The implicit differentiation calculator is a tool that helps you find the derivative of an implicit function quickly and correctly. If we think of δx δ x as the change in x x then δy = f (x+δx) −f (x) δ y = f (x + δ x) − f. For the given function $$$ y=f(x) $$$, point $$$ x_0 $$$ and argument change $$$ \delta x_0 $$$, the calculator will find the differential $$$. In simple terms, the differential of a function measures how the function's output changes as its input changes. Enter the differential equation in the provided input box. How to use the differential equation calculator?
Enter the differential equation in the provided input box. The implicit differentiation calculator is a tool that helps you find the derivative of an implicit function quickly and correctly. If we think of δx δ x as the change in x x then δy = f (x+δx) −f (x) δ y = f (x + δ x) − f. How to use the differential equation calculator? For the given function $$$ y=f(x) $$$, point $$$ x_0 $$$ and argument change $$$ \delta x_0 $$$, the calculator will find the differential $$$. In simple terms, the differential of a function measures how the function's output changes as its input changes. If you have a function y = f. Type in any function derivative to get the solution, steps and graph. To find the differential `dy`, we just need to find the derivative and write it with `dx` on the right. Example 2 find the differential `dy` of the.
If you have a function y = f. For the given function $$$ y=f(x) $$$, point $$$ x_0 $$$ and argument change $$$ \delta x_0 $$$, the calculator will find the differential $$$. If we think of δx δ x as the change in x x then δy = f (x+δx) −f (x) δ y = f (x + δ x) − f. In simple terms, the differential of a function measures how the function's output changes as its input changes. To find the differential `dy`, we just need to find the derivative and write it with `dx` on the right. How to use the differential equation calculator? Type in any function derivative to get the solution, steps and graph. Example 2 find the differential `dy` of the. If necessary, enter the initial conditions. The implicit differentiation calculator is a tool that helps you find the derivative of an implicit function quickly and correctly.
Differential (dy) Notation and Intuition Expii
There is a nice application to differentials. How to use the differential equation calculator? For the given function $$$ y=f(x) $$$, point $$$ x_0 $$$ and argument change $$$ \delta x_0 $$$, the calculator will find the differential $$$. Enter the differential equation in the provided input box. If you have a function y = f.
[Solved] a) find the differential dy. b) evaluate dy for the givin
Example 2 find the differential `dy` of the. To find the differential `dy`, we just need to find the derivative and write it with `dx` on the right. How to use the differential equation calculator? In simple terms, the differential of a function measures how the function's output changes as its input changes. The implicit differentiation calculator is a tool.
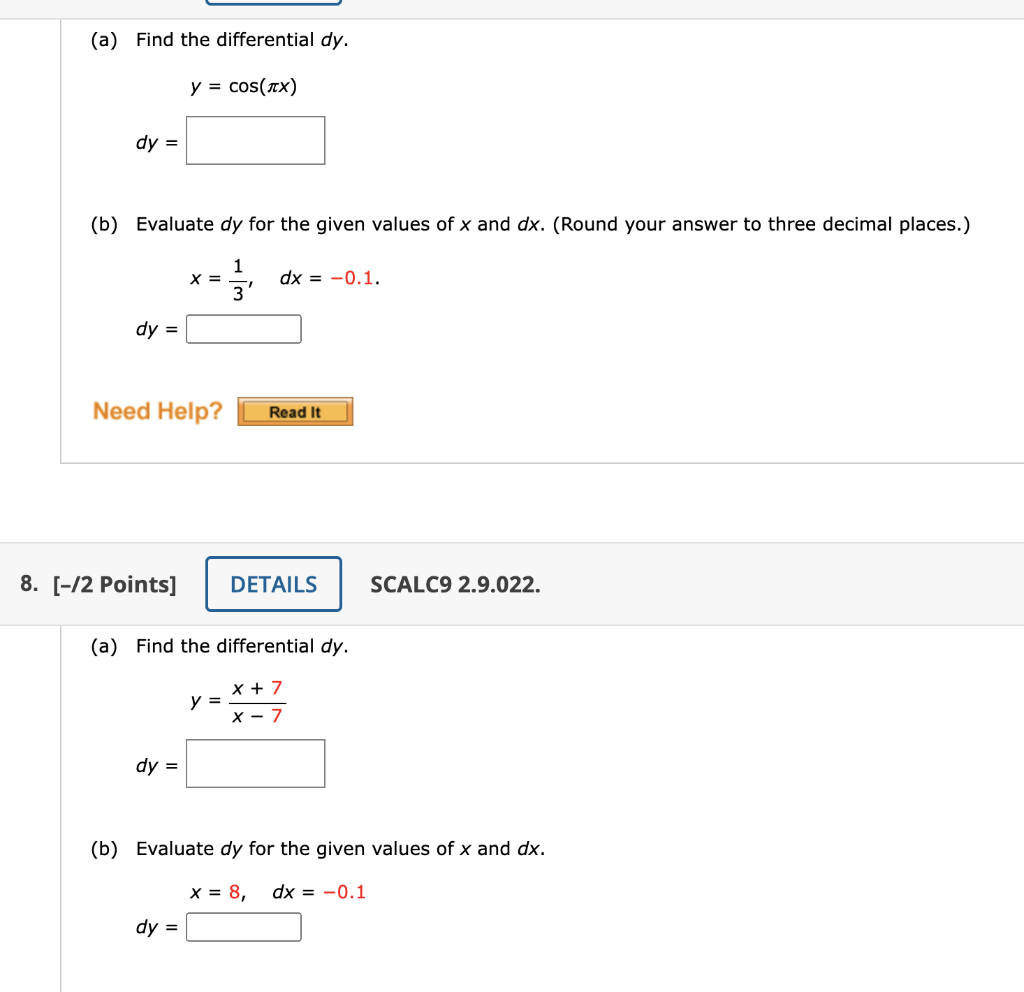
Solved (a) Find the differential dy. y = cos(ix) dy = (b)
Enter the differential equation in the provided input box. To find the differential `dy`, we just need to find the derivative and write it with `dx` on the right. For the given function $$$ y=f(x) $$$, point $$$ x_0 $$$ and argument change $$$ \delta x_0 $$$, the calculator will find the differential $$$. In simple terms, the differential of.
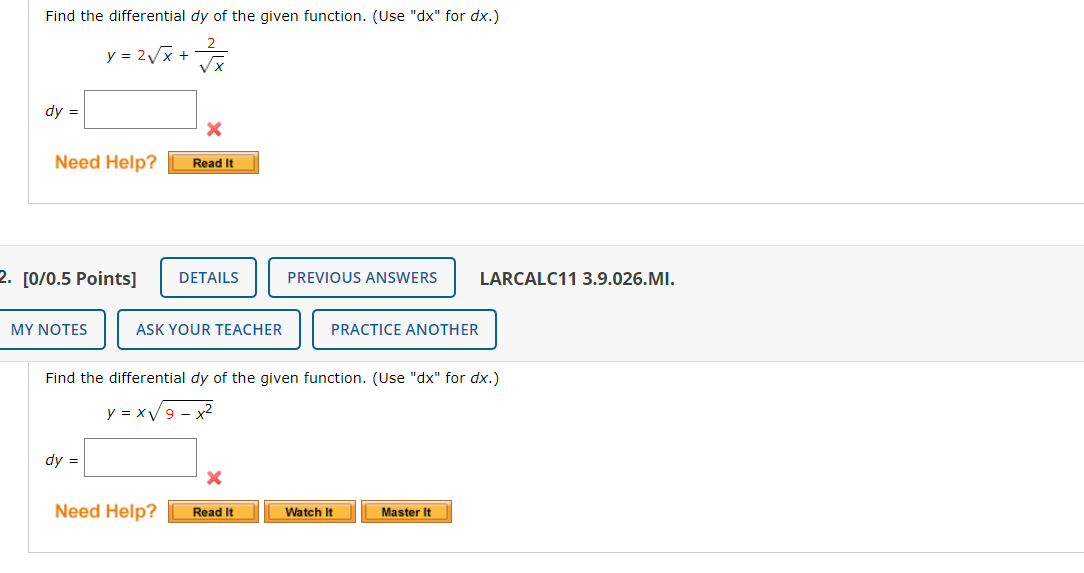
Solved find the differential dy of the given function. (Use
How to use the differential equation calculator? Enter the differential equation in the provided input box. In simple terms, the differential of a function measures how the function's output changes as its input changes. For the given function $$$ y=f(x) $$$, point $$$ x_0 $$$ and argument change $$$ \delta x_0 $$$, the calculator will find the differential $$$. If.
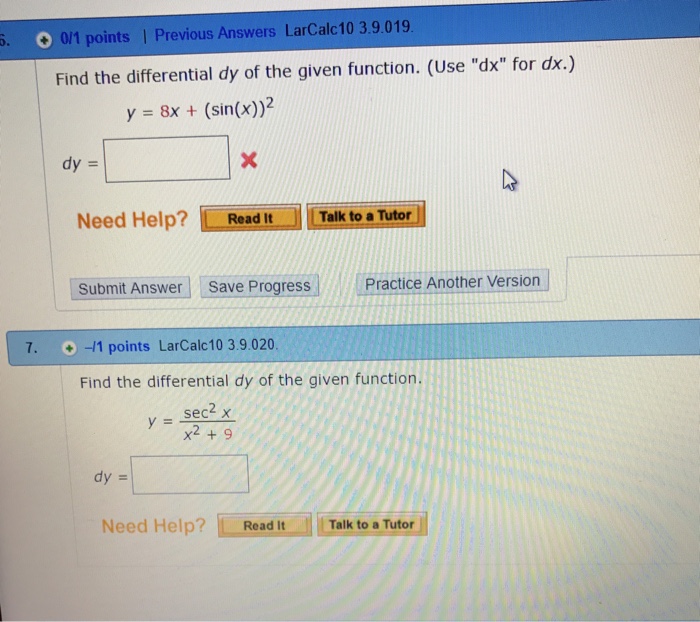
Solved Find the differential dy of the given function. (Use
The implicit differentiation calculator is a tool that helps you find the derivative of an implicit function quickly and correctly. Enter the differential equation in the provided input box. If we think of δx δ x as the change in x x then δy = f (x+δx) −f (x) δ y = f (x + δ x) − f. If.
Solved Find the differential dy of the given function. (Use
To find the differential `dy`, we just need to find the derivative and write it with `dx` on the right. Example 2 find the differential `dy` of the. How to use the differential equation calculator? Enter the differential equation in the provided input box. Type in any function derivative to get the solution, steps and graph.
Solved Find the differential dy of the given function. (Use
There is a nice application to differentials. In simple terms, the differential of a function measures how the function's output changes as its input changes. The implicit differentiation calculator is a tool that helps you find the derivative of an implicit function quickly and correctly. If we think of δx δ x as the change in x x then δy.
Solved Find the differential dy of the given function. y =
The implicit differentiation calculator is a tool that helps you find the derivative of an implicit function quickly and correctly. In simple terms, the differential of a function measures how the function's output changes as its input changes. To find the differential `dy`, we just need to find the derivative and write it with `dx` on the right. If we.
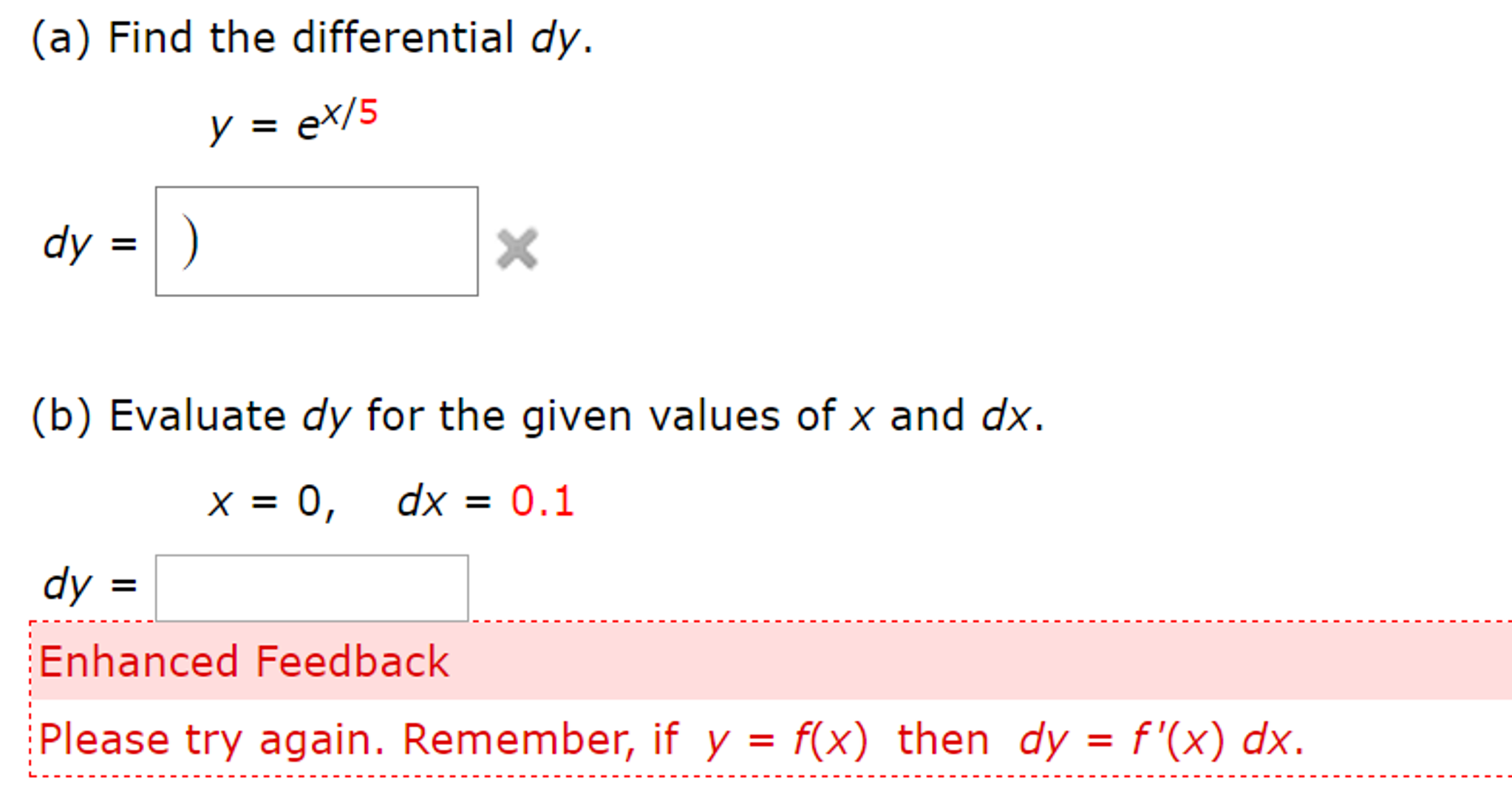
Solved Find the differential dy. Y = e^x/5 Evaluate dy for
Enter the differential equation in the provided input box. In simple terms, the differential of a function measures how the function's output changes as its input changes. To find the differential `dy`, we just need to find the derivative and write it with `dx` on the right. For the given function $$$ y=f(x) $$$, point $$$ x_0 $$$ and argument.
Solved Find the differential dy of the given function. y =
If we think of δx δ x as the change in x x then δy = f (x+δx) −f (x) δ y = f (x + δ x) − f. Example 2 find the differential `dy` of the. Type in any function derivative to get the solution, steps and graph. To find the differential `dy`, we just need to find.
There Is A Nice Application To Differentials.
If we think of δx δ x as the change in x x then δy = f (x+δx) −f (x) δ y = f (x + δ x) − f. How to use the differential equation calculator? Enter the differential equation in the provided input box. The implicit differentiation calculator is a tool that helps you find the derivative of an implicit function quickly and correctly.
If Necessary, Enter The Initial Conditions.
Example 2 find the differential `dy` of the. In simple terms, the differential of a function measures how the function's output changes as its input changes. Type in any function derivative to get the solution, steps and graph. If you have a function y = f.
To Find The Differential `Dy`, We Just Need To Find The Derivative And Write It With `Dx` On The Right.
For the given function $$$ y=f(x) $$$, point $$$ x_0 $$$ and argument change $$$ \delta x_0 $$$, the calculator will find the differential $$$.