Finding The Particular Solution To A Non-Homogeneous Differential Equation

Finding The Particular Solution To A Non-Homogeneous Differential Equation - Y p(x)y' q(x)y 0 2. In this section we will discuss the basics of solving nonhomogeneous differential equations. In this section we introduce the method of variation of parameters to find particular solutions to nonhomogeneous. We define the complimentary and. Determine the general solution y h c 1 y(x) c 2 y(x) to a homogeneous second order differential equation: In this section we introduce the method of undetermined coefficients to find particular solutions to nonhomogeneous. The final solution is the sum of the.

We define the complimentary and. In this section we introduce the method of undetermined coefficients to find particular solutions to nonhomogeneous. Y p(x)y' q(x)y 0 2. In this section we will discuss the basics of solving nonhomogeneous differential equations. In this section we introduce the method of variation of parameters to find particular solutions to nonhomogeneous. Determine the general solution y h c 1 y(x) c 2 y(x) to a homogeneous second order differential equation: The final solution is the sum of the.

Y p(x)y' q(x)y 0 2. We define the complimentary and. Determine the general solution y h c 1 y(x) c 2 y(x) to a homogeneous second order differential equation: In this section we introduce the method of variation of parameters to find particular solutions to nonhomogeneous. In this section we will discuss the basics of solving nonhomogeneous differential equations. In this section we introduce the method of undetermined coefficients to find particular solutions to nonhomogeneous. The final solution is the sum of the.

Particular Solution of NonHomogeneous Differential Equations Mr

In this section we will discuss the basics of solving nonhomogeneous differential equations. We define the complimentary and. The final solution is the sum of the. Y p(x)y' q(x)y 0 2. Determine the general solution y h c 1 y(x) c 2 y(x) to a homogeneous second order differential equation:

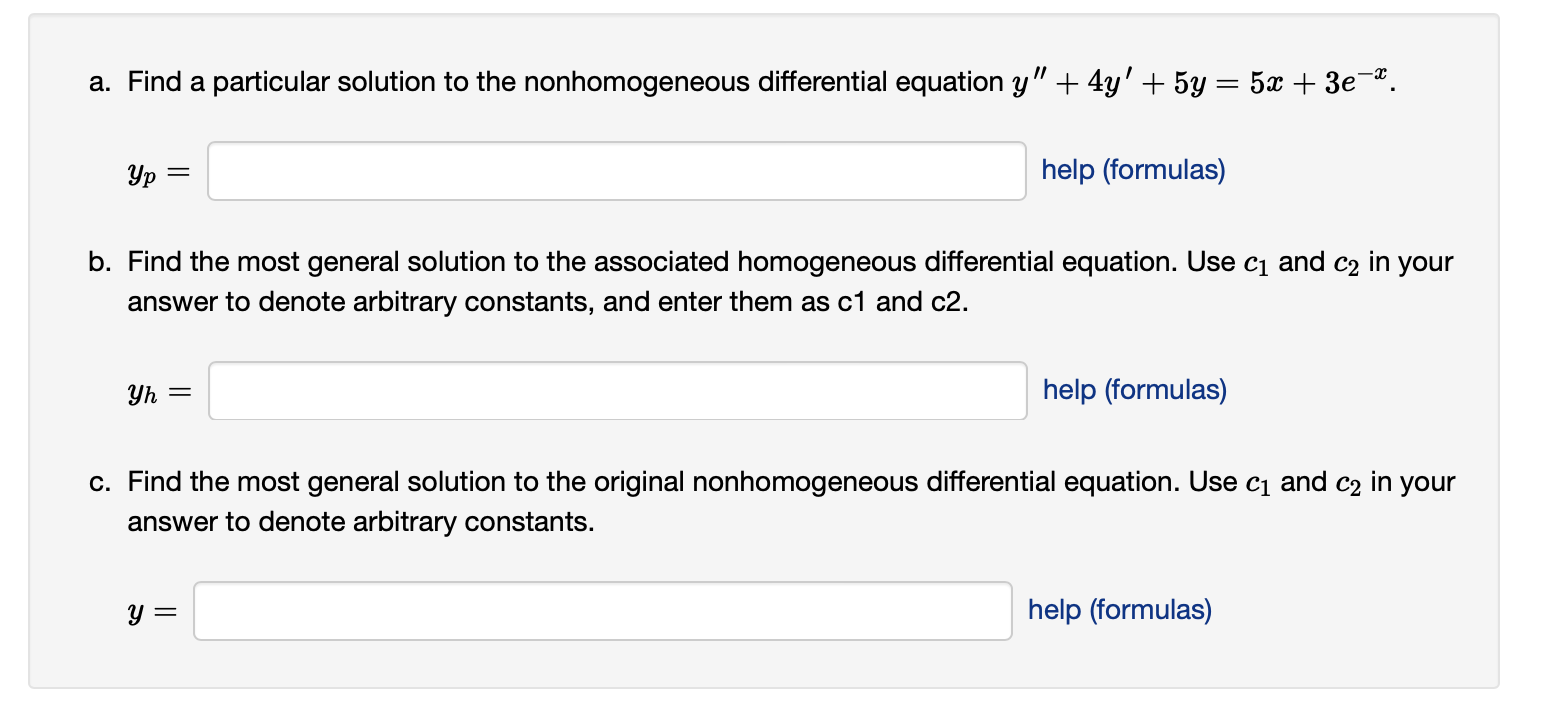
Solved (3 points) Find a particular solution to the

We define the complimentary and. In this section we introduce the method of undetermined coefficients to find particular solutions to nonhomogeneous. Determine the general solution y h c 1 y(x) c 2 y(x) to a homogeneous second order differential equation: In this section we will discuss the basics of solving nonhomogeneous differential equations. The final solution is the sum of.

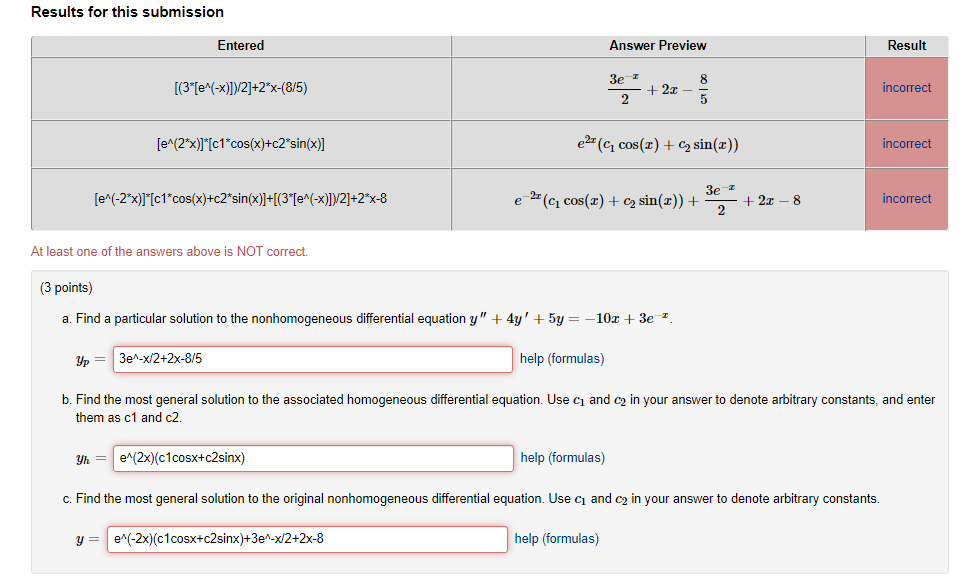
[Solved] In this problem you will solve the nonho SolutionInn

In this section we introduce the method of undetermined coefficients to find particular solutions to nonhomogeneous. In this section we will discuss the basics of solving nonhomogeneous differential equations. In this section we introduce the method of variation of parameters to find particular solutions to nonhomogeneous. The final solution is the sum of the. Determine the general solution y h.

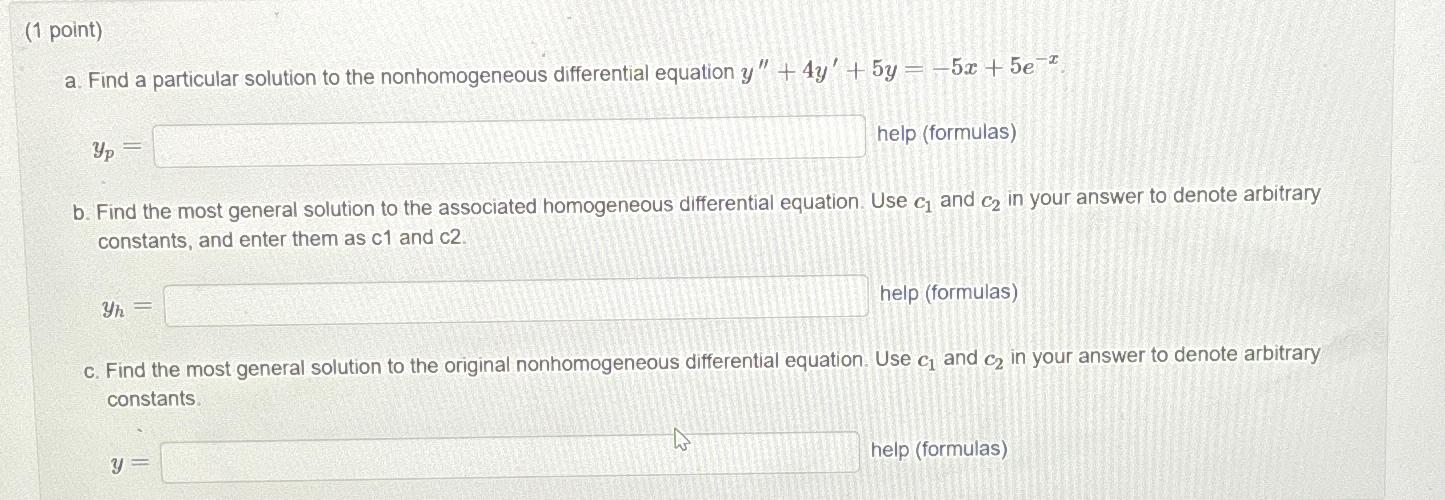
Solved (1 point)a. Find a particular solution to the

Y p(x)y' q(x)y 0 2. The final solution is the sum of the. Determine the general solution y h c 1 y(x) c 2 y(x) to a homogeneous second order differential equation: We define the complimentary and. In this section we introduce the method of undetermined coefficients to find particular solutions to nonhomogeneous.

Difference Equation Particular Solution Examples Tessshebaylo

In this section we will discuss the basics of solving nonhomogeneous differential equations. The final solution is the sum of the. Y p(x)y' q(x)y 0 2. Determine the general solution y h c 1 y(x) c 2 y(x) to a homogeneous second order differential equation: We define the complimentary and.

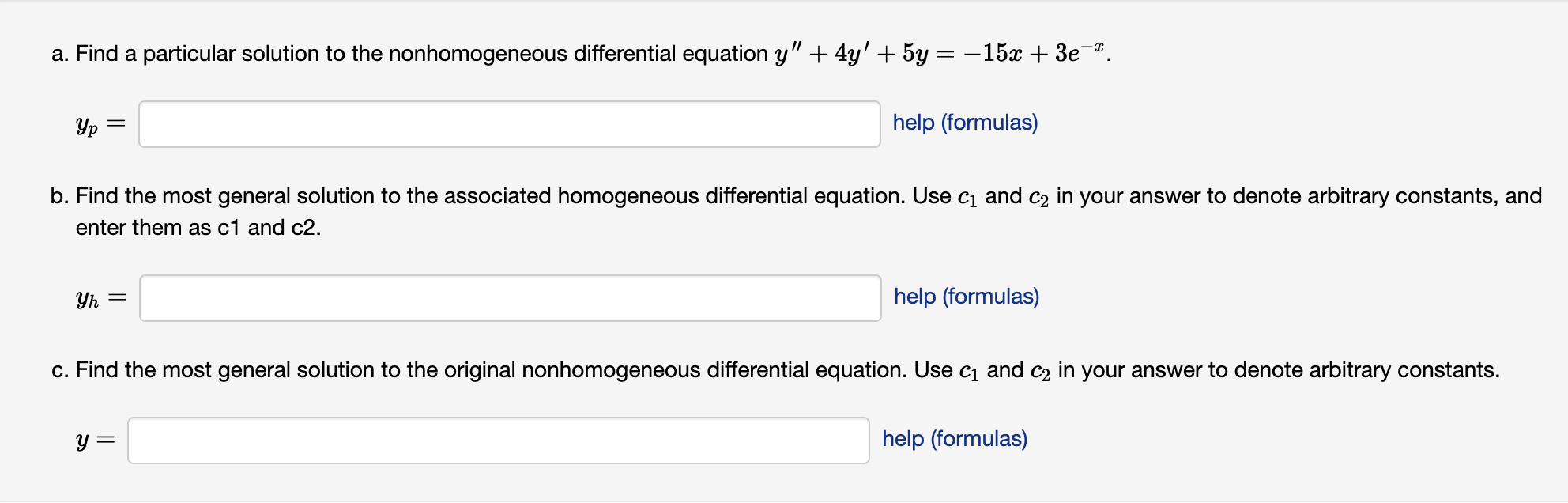
Solved a. Find a particular solution to the nonhomogeneous

Determine the general solution y h c 1 y(x) c 2 y(x) to a homogeneous second order differential equation: Y p(x)y' q(x)y 0 2. In this section we introduce the method of undetermined coefficients to find particular solutions to nonhomogeneous. In this section we introduce the method of variation of parameters to find particular solutions to nonhomogeneous. The final solution.

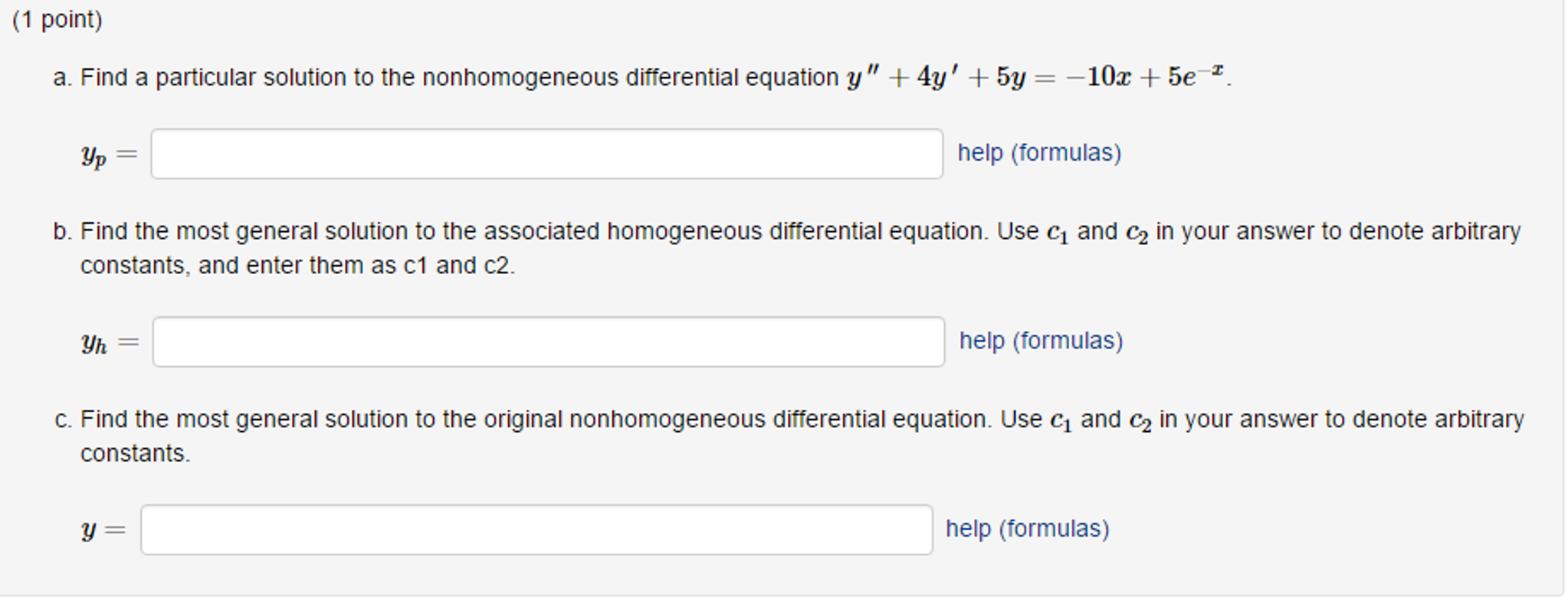
Solved Find a particular solution to the nonhomogeneous

We define the complimentary and. In this section we introduce the method of undetermined coefficients to find particular solutions to nonhomogeneous. Determine the general solution y h c 1 y(x) c 2 y(x) to a homogeneous second order differential equation: In this section we introduce the method of variation of parameters to find particular solutions to nonhomogeneous. Y p(x)y' q(x)y.

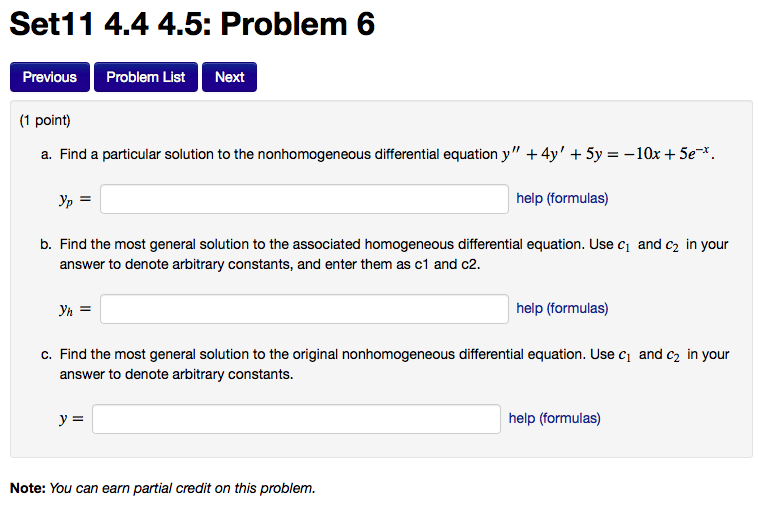
Solved Find a particular solution to the nonhomogeneous

In this section we will discuss the basics of solving nonhomogeneous differential equations. In this section we introduce the method of variation of parameters to find particular solutions to nonhomogeneous. Determine the general solution y h c 1 y(x) c 2 y(x) to a homogeneous second order differential equation: The final solution is the sum of the. We define the.

Solved Find the general solution of the nonhomogeneous

In this section we introduce the method of variation of parameters to find particular solutions to nonhomogeneous. In this section we will discuss the basics of solving nonhomogeneous differential equations. The final solution is the sum of the. We define the complimentary and. In this section we introduce the method of undetermined coefficients to find particular solutions to nonhomogeneous.

Solved a. Find a particular solution to the nonhomogeneous

In this section we introduce the method of undetermined coefficients to find particular solutions to nonhomogeneous. The final solution is the sum of the. Determine the general solution y h c 1 y(x) c 2 y(x) to a homogeneous second order differential equation: In this section we will discuss the basics of solving nonhomogeneous differential equations. Y p(x)y' q(x)y 0.

In This Section We Introduce The Method Of Undetermined Coefficients To Find Particular Solutions To Nonhomogeneous.

Determine the general solution y h c 1 y(x) c 2 y(x) to a homogeneous second order differential equation: Y p(x)y' q(x)y 0 2. We define the complimentary and. The final solution is the sum of the.