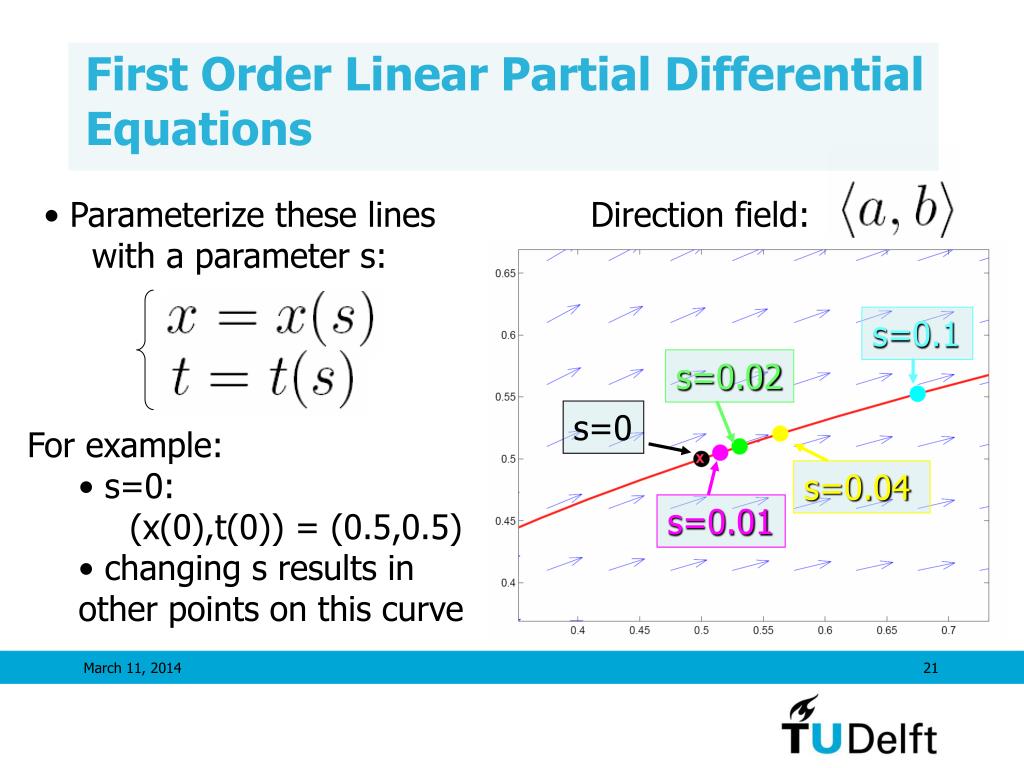
First Order Partial Differential Equations - Consider a first order pde of the form a(x,y) ∂u ∂x +b(x,y) ∂u ∂y = c(x,y,u). We have spent time solving quasilinear first order partial differential equations. We now turn to nonlinear first order equations of the form \[f(x,. Before doing so, we need to define a few terms. We are concerned in the course with partial di erential equations with one dependent variable z and mostly two independent variables x and y. We begin our study of partial differential equations with first order partial differential equations. (5) when a(x,y) and b(x,y) are constants, a linear change of variables can. See examples of linear, semilinear, quasilinear.
We are concerned in the course with partial di erential equations with one dependent variable z and mostly two independent variables x and y. We now turn to nonlinear first order equations of the form \[f(x,. We begin our study of partial differential equations with first order partial differential equations. See examples of linear, semilinear, quasilinear. We have spent time solving quasilinear first order partial differential equations. (5) when a(x,y) and b(x,y) are constants, a linear change of variables can. Before doing so, we need to define a few terms. Consider a first order pde of the form a(x,y) ∂u ∂x +b(x,y) ∂u ∂y = c(x,y,u).
We are concerned in the course with partial di erential equations with one dependent variable z and mostly two independent variables x and y. Before doing so, we need to define a few terms. We now turn to nonlinear first order equations of the form \[f(x,. (5) when a(x,y) and b(x,y) are constants, a linear change of variables can. See examples of linear, semilinear, quasilinear. We have spent time solving quasilinear first order partial differential equations. Consider a first order pde of the form a(x,y) ∂u ∂x +b(x,y) ∂u ∂y = c(x,y,u). We begin our study of partial differential equations with first order partial differential equations.
First Order Partial Differential Equations Method of Characteristics
We begin our study of partial differential equations with first order partial differential equations. (5) when a(x,y) and b(x,y) are constants, a linear change of variables can. Consider a first order pde of the form a(x,y) ∂u ∂x +b(x,y) ∂u ∂y = c(x,y,u). We now turn to nonlinear first order equations of the form \[f(x,. Before doing so, we need.
PPT First Order Partial Differential Equations PowerPoint
We begin our study of partial differential equations with first order partial differential equations. Consider a first order pde of the form a(x,y) ∂u ∂x +b(x,y) ∂u ∂y = c(x,y,u). We have spent time solving quasilinear first order partial differential equations. See examples of linear, semilinear, quasilinear. We are concerned in the course with partial di erential equations with one.
PPT First Order Partial Differential Equations PowerPoint
Before doing so, we need to define a few terms. We have spent time solving quasilinear first order partial differential equations. We begin our study of partial differential equations with first order partial differential equations. (5) when a(x,y) and b(x,y) are constants, a linear change of variables can. See examples of linear, semilinear, quasilinear.
First Order Partial Differential Equations PDF
See examples of linear, semilinear, quasilinear. We begin our study of partial differential equations with first order partial differential equations. Before doing so, we need to define a few terms. (5) when a(x,y) and b(x,y) are constants, a linear change of variables can. We now turn to nonlinear first order equations of the form \[f(x,.
First Order Differential Equation Worksheet Equations Worksheets
We have spent time solving quasilinear first order partial differential equations. We are concerned in the course with partial di erential equations with one dependent variable z and mostly two independent variables x and y. (5) when a(x,y) and b(x,y) are constants, a linear change of variables can. Before doing so, we need to define a few terms. See examples.
PPT First Order Partial Differential Equations PowerPoint
Before doing so, we need to define a few terms. See examples of linear, semilinear, quasilinear. We now turn to nonlinear first order equations of the form \[f(x,. Consider a first order pde of the form a(x,y) ∂u ∂x +b(x,y) ∂u ∂y = c(x,y,u). We are concerned in the course with partial di erential equations with one dependent variable z.
PPT First Order Partial Differential Equations PowerPoint
We are concerned in the course with partial di erential equations with one dependent variable z and mostly two independent variables x and y. (5) when a(x,y) and b(x,y) are constants, a linear change of variables can. Before doing so, we need to define a few terms. We begin our study of partial differential equations with first order partial differential.
PPT First Order Partial Differential Equations PowerPoint
(5) when a(x,y) and b(x,y) are constants, a linear change of variables can. Before doing so, we need to define a few terms. See examples of linear, semilinear, quasilinear. We begin our study of partial differential equations with first order partial differential equations. We have spent time solving quasilinear first order partial differential equations.
PPT First Order Partial Differential Equations PowerPoint
See examples of linear, semilinear, quasilinear. (5) when a(x,y) and b(x,y) are constants, a linear change of variables can. Consider a first order pde of the form a(x,y) ∂u ∂x +b(x,y) ∂u ∂y = c(x,y,u). We are concerned in the course with partial di erential equations with one dependent variable z and mostly two independent variables x and y. We.
PPT First Order Partial Differential Equations PowerPoint
We have spent time solving quasilinear first order partial differential equations. We now turn to nonlinear first order equations of the form \[f(x,. See examples of linear, semilinear, quasilinear. We begin our study of partial differential equations with first order partial differential equations. Consider a first order pde of the form a(x,y) ∂u ∂x +b(x,y) ∂u ∂y = c(x,y,u).
See Examples Of Linear, Semilinear, Quasilinear.
Before doing so, we need to define a few terms. (5) when a(x,y) and b(x,y) are constants, a linear change of variables can. We begin our study of partial differential equations with first order partial differential equations. We are concerned in the course with partial di erential equations with one dependent variable z and mostly two independent variables x and y.
Consider A First Order Pde Of The Form A(X,Y) ∂U ∂X +B(X,Y) ∂U ∂Y = C(X,Y,U).
We now turn to nonlinear first order equations of the form \[f(x,. We have spent time solving quasilinear first order partial differential equations.