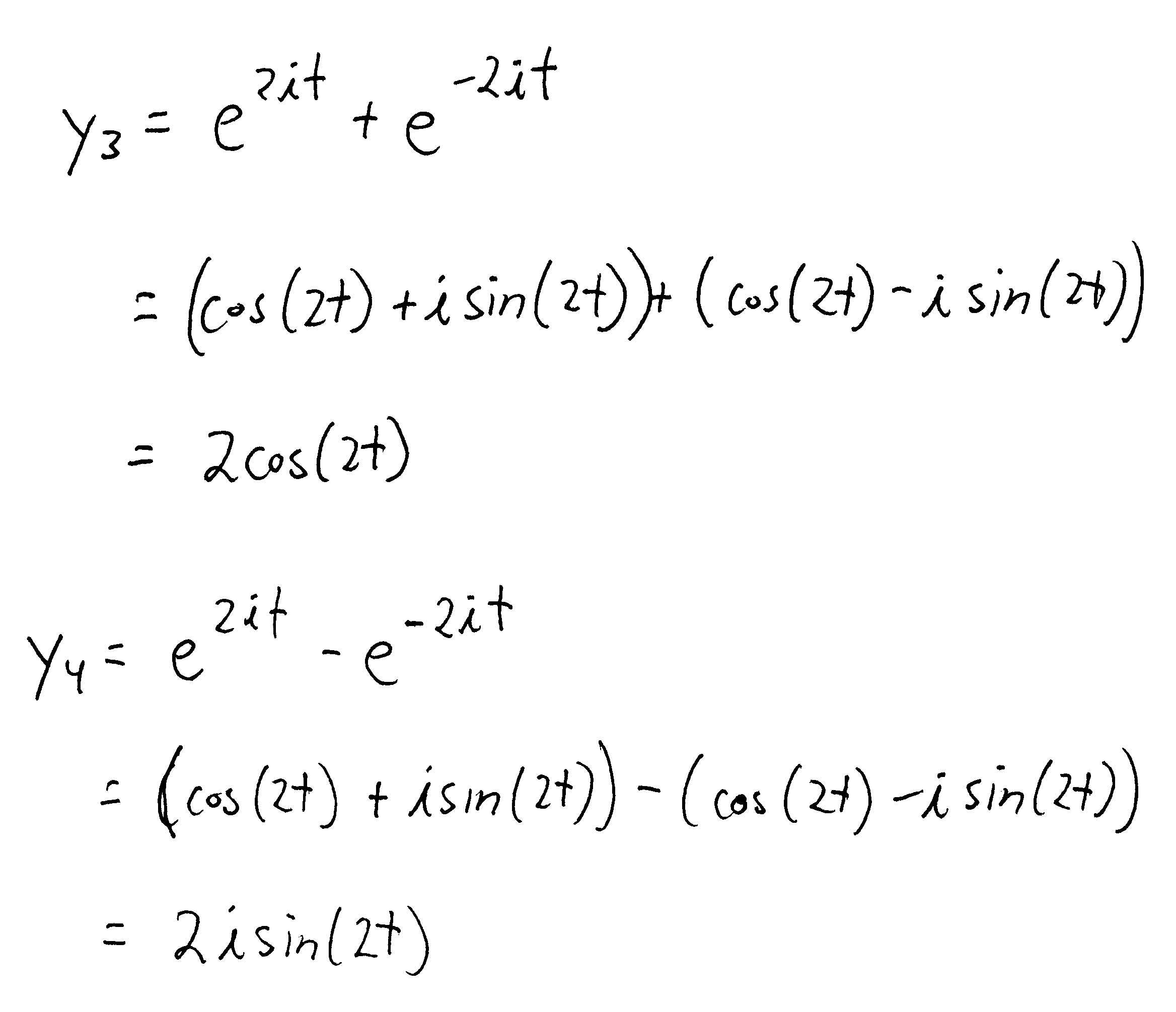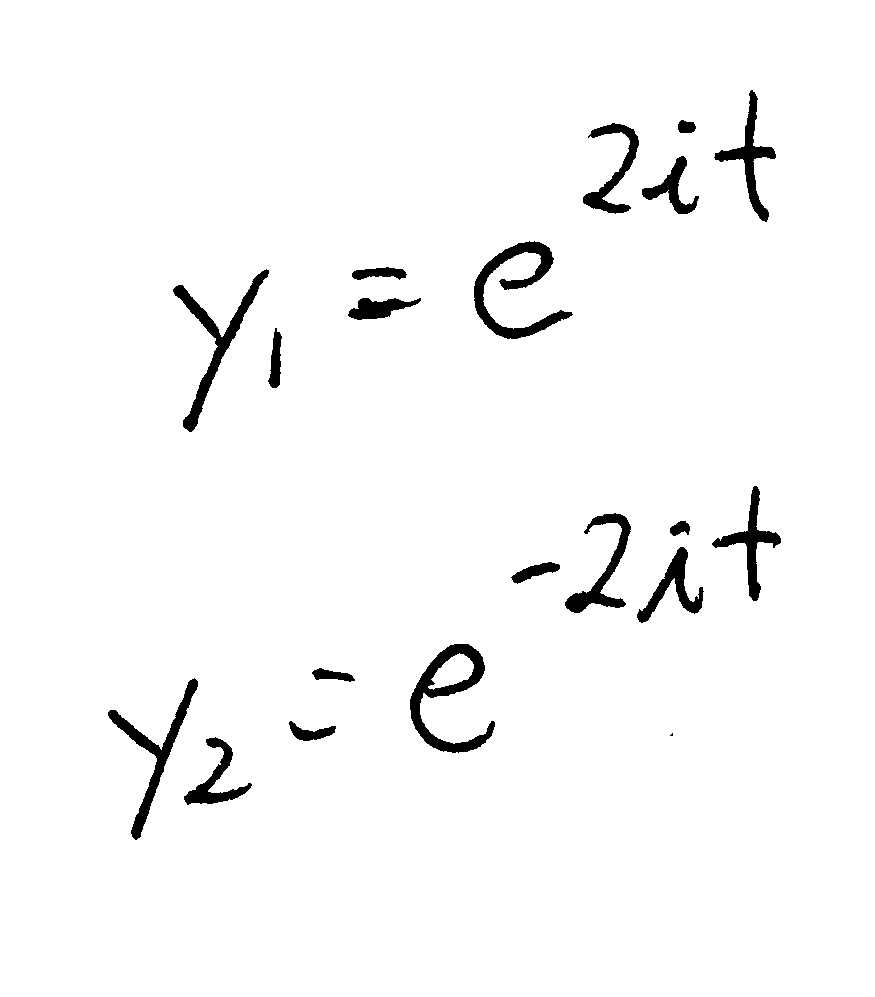Homogeneous Differential Equation Second Order - A linear nonhomogeneous differential equation of second order is represented by; A linear homogeneous second order ode with constant coefficients is an ordinary differential equation in the form: The general solution of a homogeneous linear second order equation. If \(y_1\) and \(y_2\) are defined on an interval \((a,b)\) and \(c_1\) and. Second order (the highest derivative is of. We define fundamental sets of solutions and discuss how they can be used to get a general solution to a homogeneous second. A d2y dx2 +b dy dx +cy = 0. In this tutorial, we will practise solving equations of the form:
We define fundamental sets of solutions and discuss how they can be used to get a general solution to a homogeneous second. The general solution of a homogeneous linear second order equation. A linear nonhomogeneous differential equation of second order is represented by; If \(y_1\) and \(y_2\) are defined on an interval \((a,b)\) and \(c_1\) and. In this tutorial, we will practise solving equations of the form: A linear homogeneous second order ode with constant coefficients is an ordinary differential equation in the form: A d2y dx2 +b dy dx +cy = 0. Second order (the highest derivative is of.
A d2y dx2 +b dy dx +cy = 0. The general solution of a homogeneous linear second order equation. Second order (the highest derivative is of. A linear homogeneous second order ode with constant coefficients is an ordinary differential equation in the form: We define fundamental sets of solutions and discuss how they can be used to get a general solution to a homogeneous second. In this tutorial, we will practise solving equations of the form: If \(y_1\) and \(y_2\) are defined on an interval \((a,b)\) and \(c_1\) and. A linear nonhomogeneous differential equation of second order is represented by;
College Park Tutors Blog Differential Equations Solving a second
A linear homogeneous second order ode with constant coefficients is an ordinary differential equation in the form: If \(y_1\) and \(y_2\) are defined on an interval \((a,b)\) and \(c_1\) and. The general solution of a homogeneous linear second order equation. Second order (the highest derivative is of. In this tutorial, we will practise solving equations of the form:
SOLUTION Second order linear homogeneous differential equation Studypool
The general solution of a homogeneous linear second order equation. Second order (the highest derivative is of. A linear nonhomogeneous differential equation of second order is represented by; A d2y dx2 +b dy dx +cy = 0. We define fundamental sets of solutions and discuss how they can be used to get a general solution to a homogeneous second.
Solved 2. Consider the following second order linear
If \(y_1\) and \(y_2\) are defined on an interval \((a,b)\) and \(c_1\) and. A d2y dx2 +b dy dx +cy = 0. We define fundamental sets of solutions and discuss how they can be used to get a general solution to a homogeneous second. A linear nonhomogeneous differential equation of second order is represented by; A linear homogeneous second order.
College Park Tutors Blog Differential Equations Solving a second
We define fundamental sets of solutions and discuss how they can be used to get a general solution to a homogeneous second. In this tutorial, we will practise solving equations of the form: A linear nonhomogeneous differential equation of second order is represented by; Second order (the highest derivative is of. A d2y dx2 +b dy dx +cy = 0.
SOLUTION Second order homogeneous linear differential equation Studypool
In this tutorial, we will practise solving equations of the form: A linear homogeneous second order ode with constant coefficients is an ordinary differential equation in the form: We define fundamental sets of solutions and discuss how they can be used to get a general solution to a homogeneous second. A d2y dx2 +b dy dx +cy = 0. The.
SOLUTION Second order homogeneous linear differential equation Studypool
We define fundamental sets of solutions and discuss how they can be used to get a general solution to a homogeneous second. A linear nonhomogeneous differential equation of second order is represented by; If \(y_1\) and \(y_2\) are defined on an interval \((a,b)\) and \(c_1\) and. Second order (the highest derivative is of. The general solution of a homogeneous linear.
Can the solutions to a homogeneous second order differential equation
If \(y_1\) and \(y_2\) are defined on an interval \((a,b)\) and \(c_1\) and. We define fundamental sets of solutions and discuss how they can be used to get a general solution to a homogeneous second. A linear nonhomogeneous differential equation of second order is represented by; In this tutorial, we will practise solving equations of the form: A d2y dx2.
Solved For a homogeneous second order differential equation
A d2y dx2 +b dy dx +cy = 0. Second order (the highest derivative is of. If \(y_1\) and \(y_2\) are defined on an interval \((a,b)\) and \(c_1\) and. We define fundamental sets of solutions and discuss how they can be used to get a general solution to a homogeneous second. In this tutorial, we will practise solving equations of.
SOLUTION Second order linear homogeneous differential equation Studypool
We define fundamental sets of solutions and discuss how they can be used to get a general solution to a homogeneous second. In this tutorial, we will practise solving equations of the form: Second order (the highest derivative is of. A linear homogeneous second order ode with constant coefficients is an ordinary differential equation in the form: If \(y_1\) and.
Solved Other questions 1. Given a homogeneous linear second
A linear homogeneous second order ode with constant coefficients is an ordinary differential equation in the form: A linear nonhomogeneous differential equation of second order is represented by; If \(y_1\) and \(y_2\) are defined on an interval \((a,b)\) and \(c_1\) and. The general solution of a homogeneous linear second order equation. We define fundamental sets of solutions and discuss how.
We Define Fundamental Sets Of Solutions And Discuss How They Can Be Used To Get A General Solution To A Homogeneous Second.
A linear nonhomogeneous differential equation of second order is represented by; A d2y dx2 +b dy dx +cy = 0. If \(y_1\) and \(y_2\) are defined on an interval \((a,b)\) and \(c_1\) and. Second order (the highest derivative is of.
The General Solution Of A Homogeneous Linear Second Order Equation.
In this tutorial, we will practise solving equations of the form: A linear homogeneous second order ode with constant coefficients is an ordinary differential equation in the form: