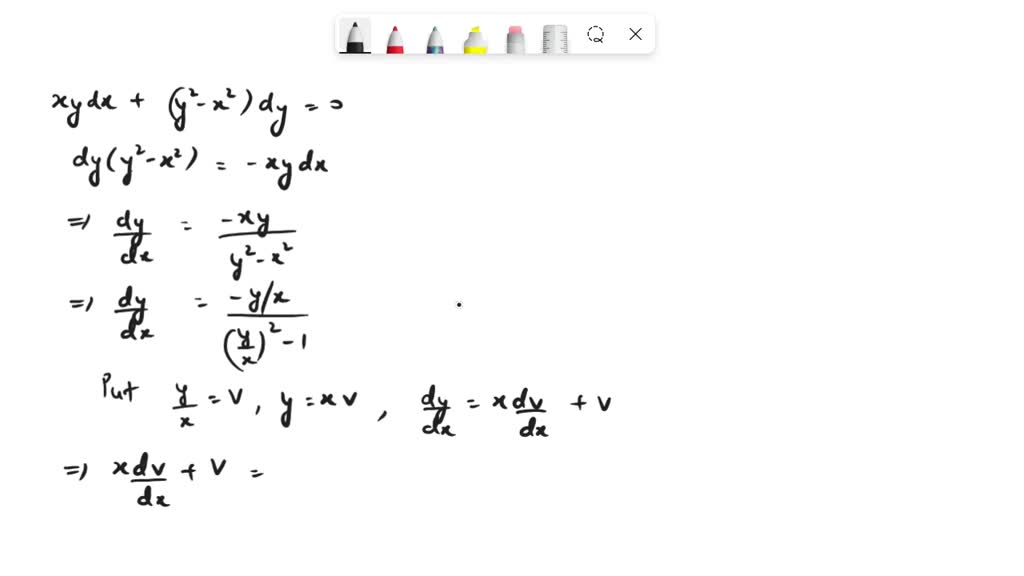Homogeneous Differential Equation - Licker's dictionary of mathematics p. 108 defines a homogeneous differential equation as. A differential equation where every scalar multiple of a solution is also a solution. Zwillinger's handbook of differential equations p. You made it clear that f(y/x) will imply that it is a division of 2 homogeneous equations of the same degree, but how does that imply that it is also the first differential dy/dx of a certain equation? Zwillinger's handbook of differential equations p. Licker's dictionary of mathematics p. 108 defines a homogeneous differential equation as. A differential equation where every scalar multiple of a solution is also a solution. If the constant gets cancelled throughout and we obtain the same equation again then that particular differential equation is homogeneous and the the power of constant which remains after cutting it to lowest degree.
A differential equation where every scalar multiple of a solution is also a solution. On a side note, are most geometric shapes we know. Licker's dictionary of mathematics p. You made it clear that f(y/x) will imply that it is a division of 2 homogeneous equations of the same degree, but how does that imply that it is also the first differential dy/dx of a certain equation? A differential equation where every scalar multiple of a solution is also a solution. Licker's dictionary of mathematics p. 108 defines a homogeneous differential equation as. 108 defines a homogeneous differential equation as. If the constant gets cancelled throughout and we obtain the same equation again then that particular differential equation is homogeneous and the the power of constant which remains after cutting it to lowest degree. Zwillinger's handbook of differential equations p.
108 defines a homogeneous differential equation as. 108 defines a homogeneous differential equation as. Zwillinger's handbook of differential equations p. You made it clear that f(y/x) will imply that it is a division of 2 homogeneous equations of the same degree, but how does that imply that it is also the first differential dy/dx of a certain equation? Zwillinger's handbook of differential equations p. Licker's dictionary of mathematics p. If the constant gets cancelled throughout and we obtain the same equation again then that particular differential equation is homogeneous and the the power of constant which remains after cutting it to lowest degree. A differential equation where every scalar multiple of a solution is also a solution. A differential equation where every scalar multiple of a solution is also a solution. Licker's dictionary of mathematics p.
Homogeneous Differential Equations HandWritten Notes in JPG Format
On a side note, are most geometric shapes we know. Licker's dictionary of mathematics p. Zwillinger's handbook of differential equations p. Licker's dictionary of mathematics p. A differential equation where every scalar multiple of a solution is also a solution.
What is Homogeneous Differential Equation? Diploma Maths Online tuition
108 defines a homogeneous differential equation as. A differential equation where every scalar multiple of a solution is also a solution. 108 defines a homogeneous differential equation as. Licker's dictionary of mathematics p. A differential equation where every scalar multiple of a solution is also a solution.
Homogeneous Differential Equation PDF Mathematical Physics Rates
Licker's dictionary of mathematics p. Zwillinger's handbook of differential equations p. A differential equation where every scalar multiple of a solution is also a solution. You made it clear that f(y/x) will imply that it is a division of 2 homogeneous equations of the same degree, but how does that imply that it is also the first differential dy/dx of.
MODULE 04 Equations of Order One Homogeneous Differential Equations
108 defines a homogeneous differential equation as. A differential equation where every scalar multiple of a solution is also a solution. Licker's dictionary of mathematics p. You made it clear that f(y/x) will imply that it is a division of 2 homogeneous equations of the same degree, but how does that imply that it is also the first differential dy/dx.
SOLVED In the given equation , solve the homogeneous differential
Zwillinger's handbook of differential equations p. Licker's dictionary of mathematics p. Licker's dictionary of mathematics p. You made it clear that f(y/x) will imply that it is a division of 2 homogeneous equations of the same degree, but how does that imply that it is also the first differential dy/dx of a certain equation? If the constant gets cancelled throughout.
Solution of Homogeneous Linear Differential equation Yawin
Zwillinger's handbook of differential equations p. Licker's dictionary of mathematics p. A differential equation where every scalar multiple of a solution is also a solution. On a side note, are most geometric shapes we know. 108 defines a homogeneous differential equation as.
Homogeneous Differential Equation2 PDF Waves Applied And
A differential equation where every scalar multiple of a solution is also a solution. Licker's dictionary of mathematics p. A differential equation where every scalar multiple of a solution is also a solution. If the constant gets cancelled throughout and we obtain the same equation again then that particular differential equation is homogeneous and the the power of constant which.
Homogeneous Differential Equation Know types, Steps to solve
Zwillinger's handbook of differential equations p. You made it clear that f(y/x) will imply that it is a division of 2 homogeneous equations of the same degree, but how does that imply that it is also the first differential dy/dx of a certain equation? If the constant gets cancelled throughout and we obtain the same equation again then that particular.
Can a differential equation be both homogeneous differential equation
Zwillinger's handbook of differential equations p. On a side note, are most geometric shapes we know. Licker's dictionary of mathematics p. 108 defines a homogeneous differential equation as. A differential equation where every scalar multiple of a solution is also a solution.
Chapter 4 Homogeneous Differential Equation PDF Differential
On a side note, are most geometric shapes we know. 108 defines a homogeneous differential equation as. If the constant gets cancelled throughout and we obtain the same equation again then that particular differential equation is homogeneous and the the power of constant which remains after cutting it to lowest degree. Zwillinger's handbook of differential equations p. 108 defines a.
Zwillinger's Handbook Of Differential Equations P.
You made it clear that f(y/x) will imply that it is a division of 2 homogeneous equations of the same degree, but how does that imply that it is also the first differential dy/dx of a certain equation? 108 defines a homogeneous differential equation as. 108 defines a homogeneous differential equation as. On a side note, are most geometric shapes we know.
Licker's Dictionary Of Mathematics P.
If the constant gets cancelled throughout and we obtain the same equation again then that particular differential equation is homogeneous and the the power of constant which remains after cutting it to lowest degree. A differential equation where every scalar multiple of a solution is also a solution. A differential equation where every scalar multiple of a solution is also a solution. Zwillinger's handbook of differential equations p.