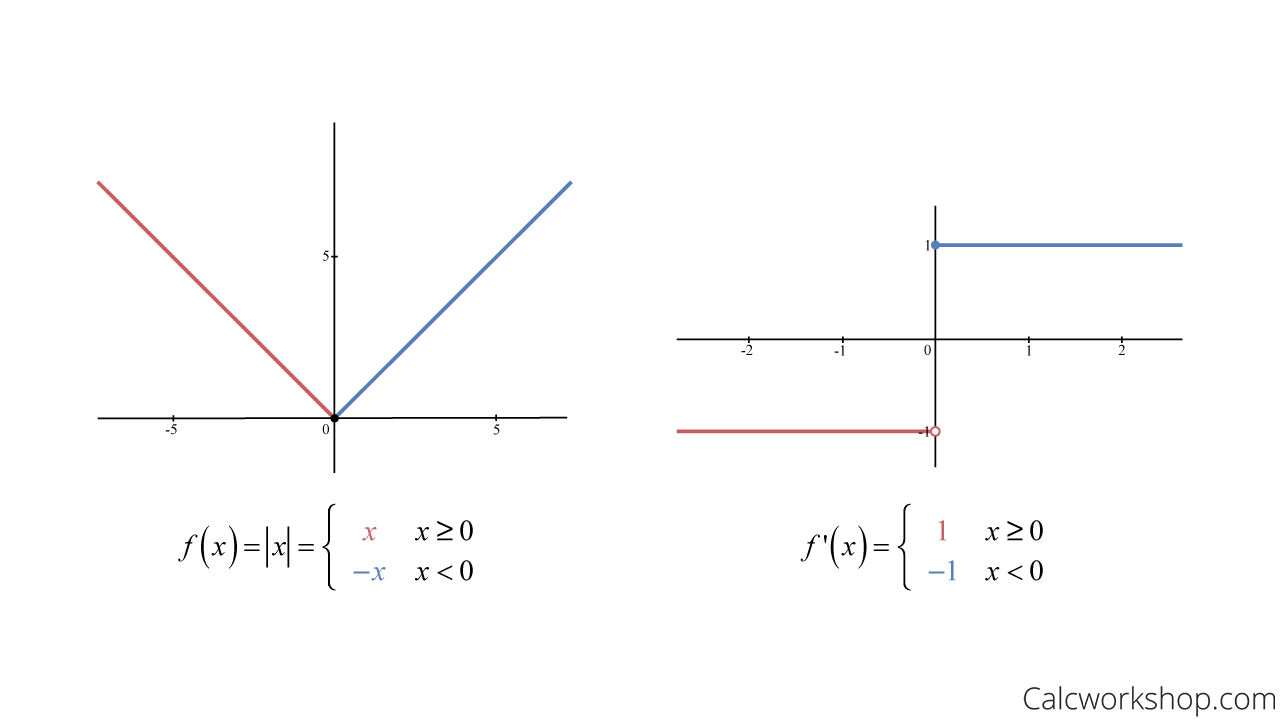
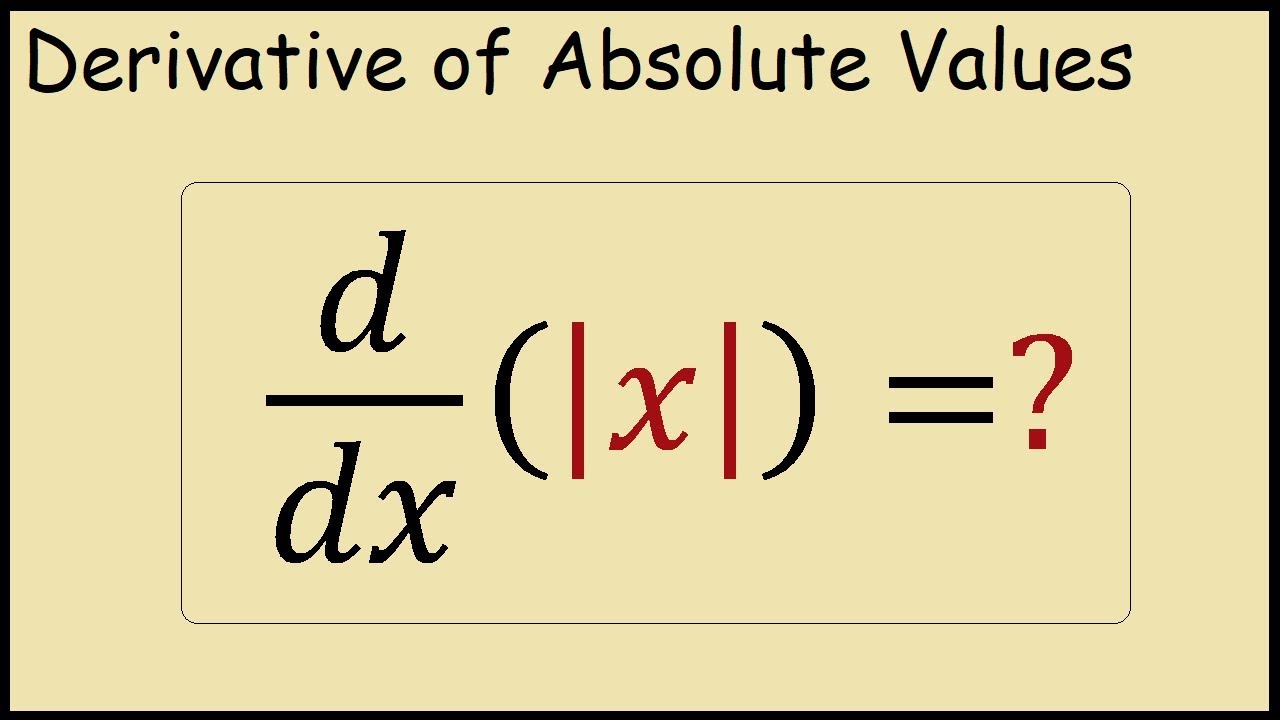How To Differentiate Absolute Values - The derivative of a function involving an absolute value can be a bit tricky due to the existence of a sharp point in the function (at the point where. Steps on how to find the derivative of the absolute value of xthe first step is to manipulate the absolute value of x into the form. Let $\size x$ be the absolute value of $x$ for real $x$. The derivative of absolute value (function) is defined as the rate of change or the slope of a function at a specific point. $\dfrac \d {\d x} \size x = \dfrac x {\size x}$ for $x \ne 0$.
Let $\size x$ be the absolute value of $x$ for real $x$. The derivative of a function involving an absolute value can be a bit tricky due to the existence of a sharp point in the function (at the point where. $\dfrac \d {\d x} \size x = \dfrac x {\size x}$ for $x \ne 0$. Steps on how to find the derivative of the absolute value of xthe first step is to manipulate the absolute value of x into the form. The derivative of absolute value (function) is defined as the rate of change or the slope of a function at a specific point.
The derivative of a function involving an absolute value can be a bit tricky due to the existence of a sharp point in the function (at the point where. $\dfrac \d {\d x} \size x = \dfrac x {\size x}$ for $x \ne 0$. The derivative of absolute value (function) is defined as the rate of change or the slope of a function at a specific point. Let $\size x$ be the absolute value of $x$ for real $x$. Steps on how to find the derivative of the absolute value of xthe first step is to manipulate the absolute value of x into the form.
How To Differentiate An Absolute Value
Let $\size x$ be the absolute value of $x$ for real $x$. The derivative of a function involving an absolute value can be a bit tricky due to the existence of a sharp point in the function (at the point where. $\dfrac \d {\d x} \size x = \dfrac x {\size x}$ for $x \ne 0$. The derivative of absolute.
How To Differentiate An Absolute Value
Let $\size x$ be the absolute value of $x$ for real $x$. The derivative of a function involving an absolute value can be a bit tricky due to the existence of a sharp point in the function (at the point where. The derivative of absolute value (function) is defined as the rate of change or the slope of a function.
Differentiate Absolute Value Function
The derivative of absolute value (function) is defined as the rate of change or the slope of a function at a specific point. $\dfrac \d {\d x} \size x = \dfrac x {\size x}$ for $x \ne 0$. Steps on how to find the derivative of the absolute value of xthe first step is to manipulate the absolute value of.
Absolute values of... Download Scientific Diagram
Steps on how to find the derivative of the absolute value of xthe first step is to manipulate the absolute value of x into the form. The derivative of absolute value (function) is defined as the rate of change or the slope of a function at a specific point. Let $\size x$ be the absolute value of $x$ for real.
SOLUTION Absolute Values Studypool
Let $\size x$ be the absolute value of $x$ for real $x$. $\dfrac \d {\d x} \size x = \dfrac x {\size x}$ for $x \ne 0$. The derivative of absolute value (function) is defined as the rate of change or the slope of a function at a specific point. The derivative of a function involving an absolute value can.
Differentiate Absolute Value Function
The derivative of absolute value (function) is defined as the rate of change or the slope of a function at a specific point. $\dfrac \d {\d x} \size x = \dfrac x {\size x}$ for $x \ne 0$. Steps on how to find the derivative of the absolute value of xthe first step is to manipulate the absolute value of.
Differentiate Absolute Value Function
$\dfrac \d {\d x} \size x = \dfrac x {\size x}$ for $x \ne 0$. Let $\size x$ be the absolute value of $x$ for real $x$. The derivative of absolute value (function) is defined as the rate of change or the slope of a function at a specific point. Steps on how to find the derivative of the absolute.
How To Differentiate An Absolute Value
The derivative of a function involving an absolute value can be a bit tricky due to the existence of a sharp point in the function (at the point where. $\dfrac \d {\d x} \size x = \dfrac x {\size x}$ for $x \ne 0$. Steps on how to find the derivative of the absolute value of xthe first step is.
Absolute Value Definition, Equation and Properties with Examples
$\dfrac \d {\d x} \size x = \dfrac x {\size x}$ for $x \ne 0$. Steps on how to find the derivative of the absolute value of xthe first step is to manipulate the absolute value of x into the form. Let $\size x$ be the absolute value of $x$ for real $x$. The derivative of a function involving an.
Differentiate Absolute Value Function
The derivative of absolute value (function) is defined as the rate of change or the slope of a function at a specific point. Steps on how to find the derivative of the absolute value of xthe first step is to manipulate the absolute value of x into the form. The derivative of a function involving an absolute value can be.
Let $\Size X$ Be The Absolute Value Of $X$ For Real $X$.
$\dfrac \d {\d x} \size x = \dfrac x {\size x}$ for $x \ne 0$. Steps on how to find the derivative of the absolute value of xthe first step is to manipulate the absolute value of x into the form. The derivative of a function involving an absolute value can be a bit tricky due to the existence of a sharp point in the function (at the point where. The derivative of absolute value (function) is defined as the rate of change or the slope of a function at a specific point.