How To Find The Differential Of A Function - The differential of a function is equal to the derivative of the function times the differential of the independent variable: In other words, \(dy\) for the first problem,. For instance, given the function \(w = g\left( {x,y,z} \right)\) the differential is given by, \[dw = {g_x}\,dx + {g_y}\,dy + {g_z}\,dz\] let’s do. Finding the differential of a function involves computing its derivative and then multiplying by a small change in the input. Know that a derivative is a calculation of the rate of change of a function. In this kind of problem we’re being asked to compute the differential of the function.
In other words, \(dy\) for the first problem,. In this kind of problem we’re being asked to compute the differential of the function. Know that a derivative is a calculation of the rate of change of a function. Finding the differential of a function involves computing its derivative and then multiplying by a small change in the input. The differential of a function is equal to the derivative of the function times the differential of the independent variable: For instance, given the function \(w = g\left( {x,y,z} \right)\) the differential is given by, \[dw = {g_x}\,dx + {g_y}\,dy + {g_z}\,dz\] let’s do.
For instance, given the function \(w = g\left( {x,y,z} \right)\) the differential is given by, \[dw = {g_x}\,dx + {g_y}\,dy + {g_z}\,dz\] let’s do. Know that a derivative is a calculation of the rate of change of a function. The differential of a function is equal to the derivative of the function times the differential of the independent variable: In this kind of problem we’re being asked to compute the differential of the function. In other words, \(dy\) for the first problem,. Finding the differential of a function involves computing its derivative and then multiplying by a small change in the input.
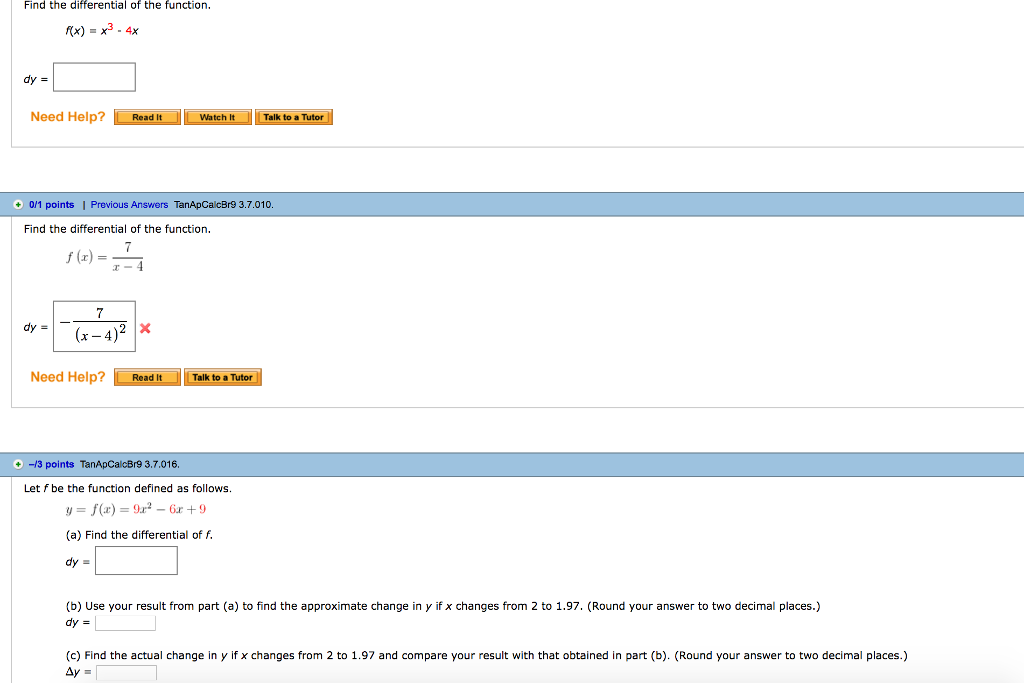
SOLVED Find the differential d y of the given function. (Use "dx" for
Finding the differential of a function involves computing its derivative and then multiplying by a small change in the input. For instance, given the function \(w = g\left( {x,y,z} \right)\) the differential is given by, \[dw = {g_x}\,dx + {g_y}\,dy + {g_z}\,dz\] let’s do. The differential of a function is equal to the derivative of the function times the differential.
Solved Find the differential dy of the given function. (Use
The differential of a function is equal to the derivative of the function times the differential of the independent variable: For instance, given the function \(w = g\left( {x,y,z} \right)\) the differential is given by, \[dw = {g_x}\,dx + {g_y}\,dy + {g_z}\,dz\] let’s do. In other words, \(dy\) for the first problem,. Know that a derivative is a calculation of.
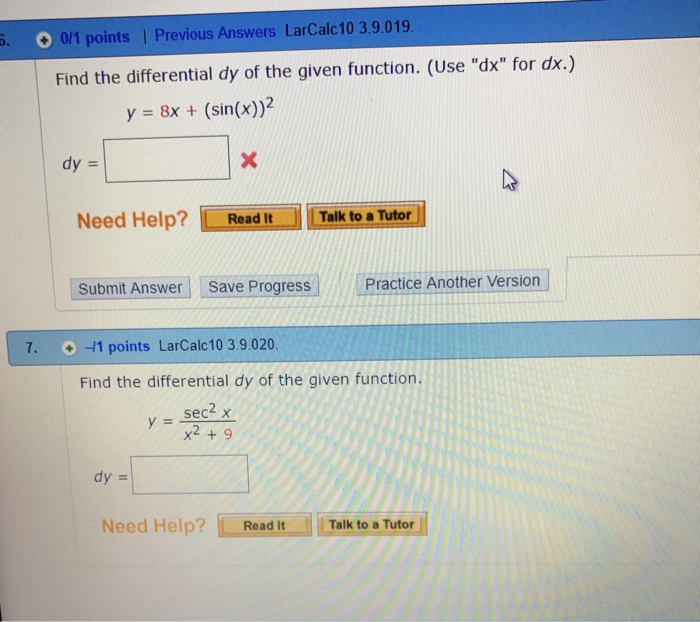
Solved Find the differential dy of the given function. y =
Finding the differential of a function involves computing its derivative and then multiplying by a small change in the input. In this kind of problem we’re being asked to compute the differential of the function. In other words, \(dy\) for the first problem,. The differential of a function is equal to the derivative of the function times the differential of.
Solved Find the differential of each function. a) y=e^tan
In this kind of problem we’re being asked to compute the differential of the function. In other words, \(dy\) for the first problem,. For instance, given the function \(w = g\left( {x,y,z} \right)\) the differential is given by, \[dw = {g_x}\,dx + {g_y}\,dy + {g_z}\,dz\] let’s do. The differential of a function is equal to the derivative of the function.
Differential Equations Owlcation
In this kind of problem we’re being asked to compute the differential of the function. Know that a derivative is a calculation of the rate of change of a function. In other words, \(dy\) for the first problem,. The differential of a function is equal to the derivative of the function times the differential of the independent variable: Finding the.
Solved Find the differential of the function. f(x) = x^2
The differential of a function is equal to the derivative of the function times the differential of the independent variable: In this kind of problem we’re being asked to compute the differential of the function. In other words, \(dy\) for the first problem,. Finding the differential of a function involves computing its derivative and then multiplying by a small change.
Solved Find the differential dy of the given function. (Use
For instance, given the function \(w = g\left( {x,y,z} \right)\) the differential is given by, \[dw = {g_x}\,dx + {g_y}\,dy + {g_z}\,dz\] let’s do. The differential of a function is equal to the derivative of the function times the differential of the independent variable: Finding the differential of a function involves computing its derivative and then multiplying by a small.
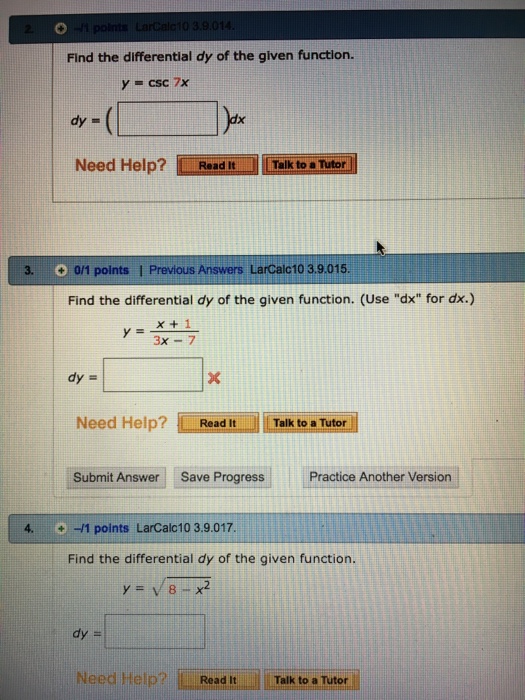
Solved Find the differential dy of the given function. y =
In this kind of problem we’re being asked to compute the differential of the function. Finding the differential of a function involves computing its derivative and then multiplying by a small change in the input. Know that a derivative is a calculation of the rate of change of a function. The differential of a function is equal to the derivative.
Solved find the differential dy of the given function. (Use
For instance, given the function \(w = g\left( {x,y,z} \right)\) the differential is given by, \[dw = {g_x}\,dx + {g_y}\,dy + {g_z}\,dz\] let’s do. In this kind of problem we’re being asked to compute the differential of the function. In other words, \(dy\) for the first problem,. The differential of a function is equal to the derivative of the function.
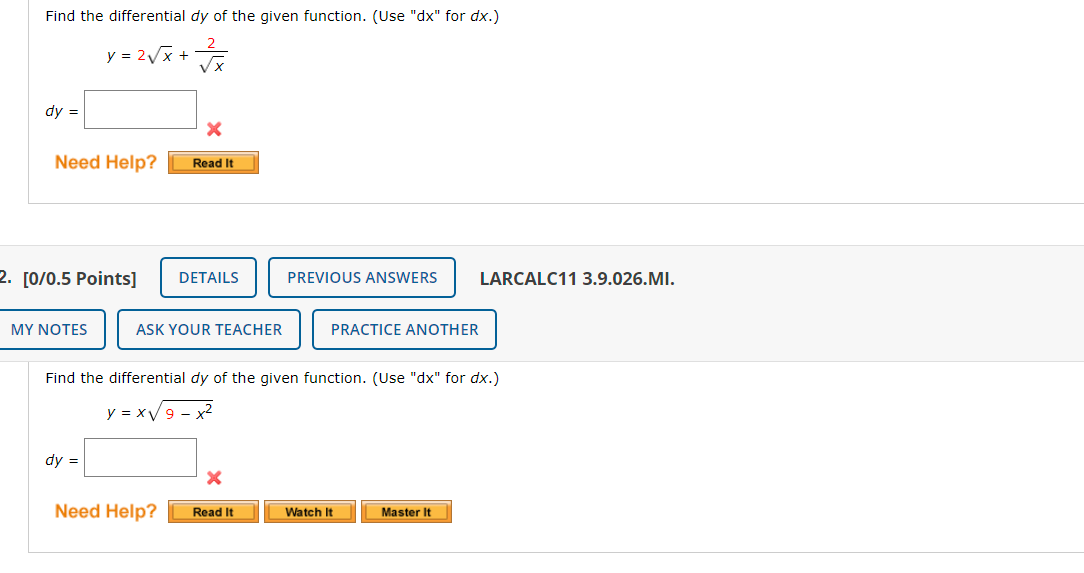
Solved Find the differential dy of the given function. (Use
For instance, given the function \(w = g\left( {x,y,z} \right)\) the differential is given by, \[dw = {g_x}\,dx + {g_y}\,dy + {g_z}\,dz\] let’s do. Finding the differential of a function involves computing its derivative and then multiplying by a small change in the input. The differential of a function is equal to the derivative of the function times the differential.
Finding The Differential Of A Function Involves Computing Its Derivative And Then Multiplying By A Small Change In The Input.
The differential of a function is equal to the derivative of the function times the differential of the independent variable: Know that a derivative is a calculation of the rate of change of a function. In other words, \(dy\) for the first problem,. For instance, given the function \(w = g\left( {x,y,z} \right)\) the differential is given by, \[dw = {g_x}\,dx + {g_y}\,dy + {g_z}\,dz\] let’s do.