How To Prove Differentiability - A function f(x) is said to be. To prove that a function is differentiable at a point $x \in \mathbb{r}$ we must prove that the limit. Differentiability and concept of differentiability. To show that $f$ is differentiable at all $x \in \bbb r$, we must show that $f'(x)$. We'll learn how to check if a function is differentiable using easy rules, understand why.
Differentiability and concept of differentiability. To prove that a function is differentiable at a point $x \in \mathbb{r}$ we must prove that the limit. We'll learn how to check if a function is differentiable using easy rules, understand why. A function f(x) is said to be. To show that $f$ is differentiable at all $x \in \bbb r$, we must show that $f'(x)$.
To prove that a function is differentiable at a point $x \in \mathbb{r}$ we must prove that the limit. We'll learn how to check if a function is differentiable using easy rules, understand why. To show that $f$ is differentiable at all $x \in \bbb r$, we must show that $f'(x)$. A function f(x) is said to be. Differentiability and concept of differentiability.
SOLUTION Continuity differentiability Studypool
We'll learn how to check if a function is differentiable using easy rules, understand why. Differentiability and concept of differentiability. To show that $f$ is differentiable at all $x \in \bbb r$, we must show that $f'(x)$. To prove that a function is differentiable at a point $x \in \mathbb{r}$ we must prove that the limit. A function f(x) is.
SOLUTION Calculus Differentiability Presentation Studypool
Differentiability and concept of differentiability. A function f(x) is said to be. To prove that a function is differentiable at a point $x \in \mathbb{r}$ we must prove that the limit. To show that $f$ is differentiable at all $x \in \bbb r$, we must show that $f'(x)$. We'll learn how to check if a function is differentiable using easy.
SOLUTION Continuity differentiability derivatives Studypool
A function f(x) is said to be. To show that $f$ is differentiable at all $x \in \bbb r$, we must show that $f'(x)$. We'll learn how to check if a function is differentiable using easy rules, understand why. To prove that a function is differentiable at a point $x \in \mathbb{r}$ we must prove that the limit. Differentiability and.
derivatives Differentiability Implies Continuity (Multivariable
To prove that a function is differentiable at a point $x \in \mathbb{r}$ we must prove that the limit. Differentiability and concept of differentiability. To show that $f$ is differentiable at all $x \in \bbb r$, we must show that $f'(x)$. We'll learn how to check if a function is differentiable using easy rules, understand why. A function f(x) is.
SOLVEDDifferentiability Implies Continuity Use the definition of
Differentiability and concept of differentiability. A function f(x) is said to be. We'll learn how to check if a function is differentiable using easy rules, understand why. To prove that a function is differentiable at a point $x \in \mathbb{r}$ we must prove that the limit. To show that $f$ is differentiable at all $x \in \bbb r$, we must.
real analysis To prove differentiability of a function at a point
Differentiability and concept of differentiability. A function f(x) is said to be. To prove that a function is differentiable at a point $x \in \mathbb{r}$ we must prove that the limit. We'll learn how to check if a function is differentiable using easy rules, understand why. To show that $f$ is differentiable at all $x \in \bbb r$, we must.
if FX is differentiable at X equal to a prove that it will be
We'll learn how to check if a function is differentiable using easy rules, understand why. To prove that a function is differentiable at a point $x \in \mathbb{r}$ we must prove that the limit. Differentiability and concept of differentiability. To show that $f$ is differentiable at all $x \in \bbb r$, we must show that $f'(x)$. A function f(x) is.
SOLVEDUse the definition of differentiability to prove that the
A function f(x) is said to be. Differentiability and concept of differentiability. We'll learn how to check if a function is differentiable using easy rules, understand why. To prove that a function is differentiable at a point $x \in \mathbb{r}$ we must prove that the limit. To show that $f$ is differentiable at all $x \in \bbb r$, we must.
Question 90 pls 90 Prove that f(x) = [1 x] + [x 1] is Maths
To show that $f$ is differentiable at all $x \in \bbb r$, we must show that $f'(x)$. To prove that a function is differentiable at a point $x \in \mathbb{r}$ we must prove that the limit. A function f(x) is said to be. We'll learn how to check if a function is differentiable using easy rules, understand why. Differentiability and.
Differentiability
To show that $f$ is differentiable at all $x \in \bbb r$, we must show that $f'(x)$. Differentiability and concept of differentiability. A function f(x) is said to be. To prove that a function is differentiable at a point $x \in \mathbb{r}$ we must prove that the limit. We'll learn how to check if a function is differentiable using easy.
We'll Learn How To Check If A Function Is Differentiable Using Easy Rules, Understand Why.
To prove that a function is differentiable at a point $x \in \mathbb{r}$ we must prove that the limit. A function f(x) is said to be. To show that $f$ is differentiable at all $x \in \bbb r$, we must show that $f'(x)$. Differentiability and concept of differentiability.




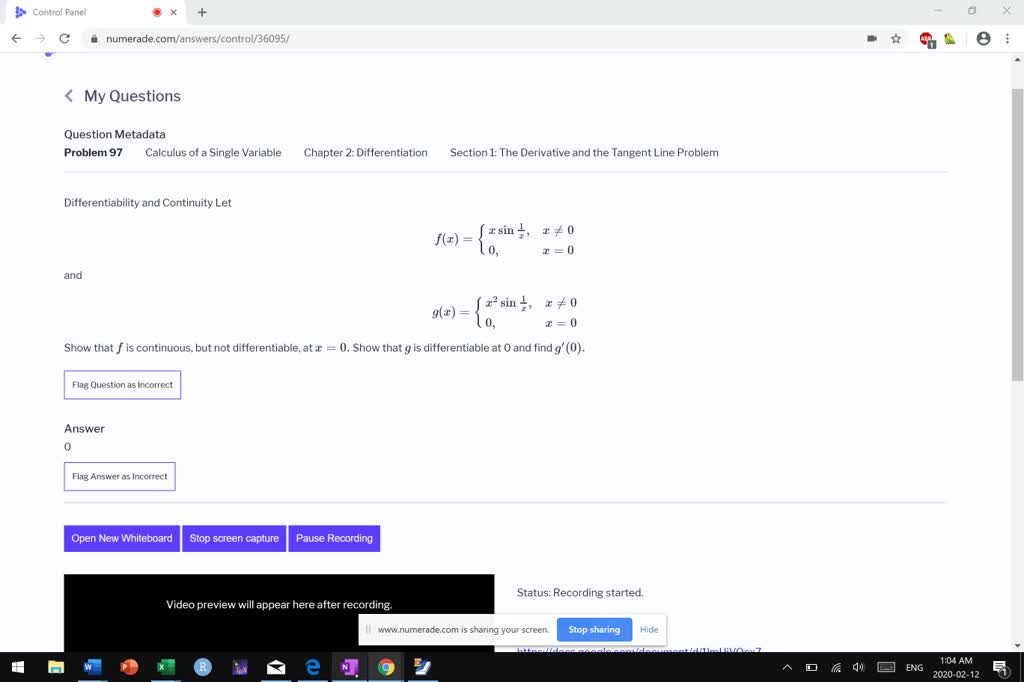


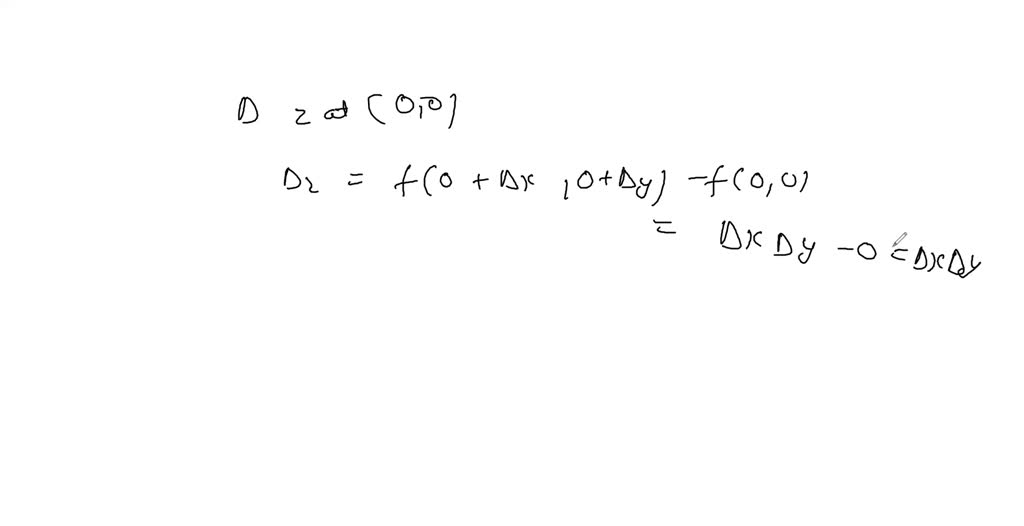
![Question 90 pls 90 Prove that f(x) = [1 x] + [x 1] is Maths](https://s3mn.mnimgs.com/img/shared/content_ck_images/ck_5d1518ae3e675.jpg)
