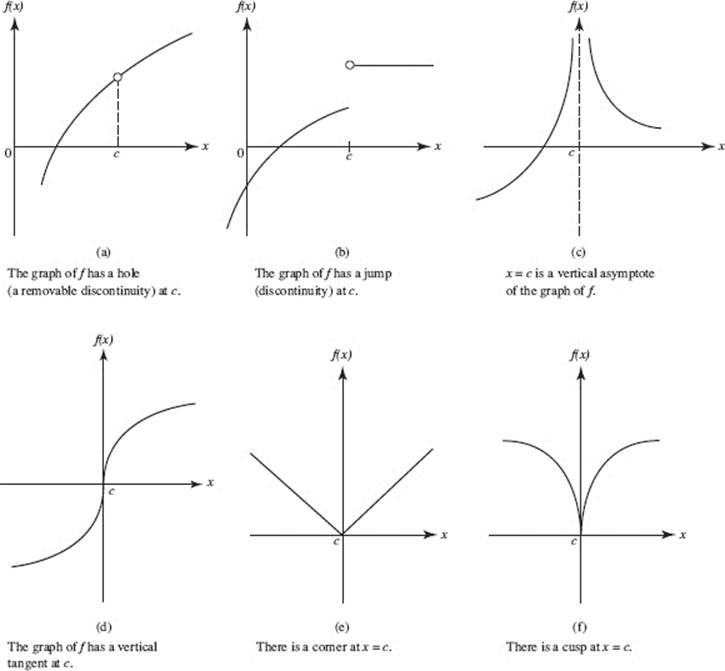
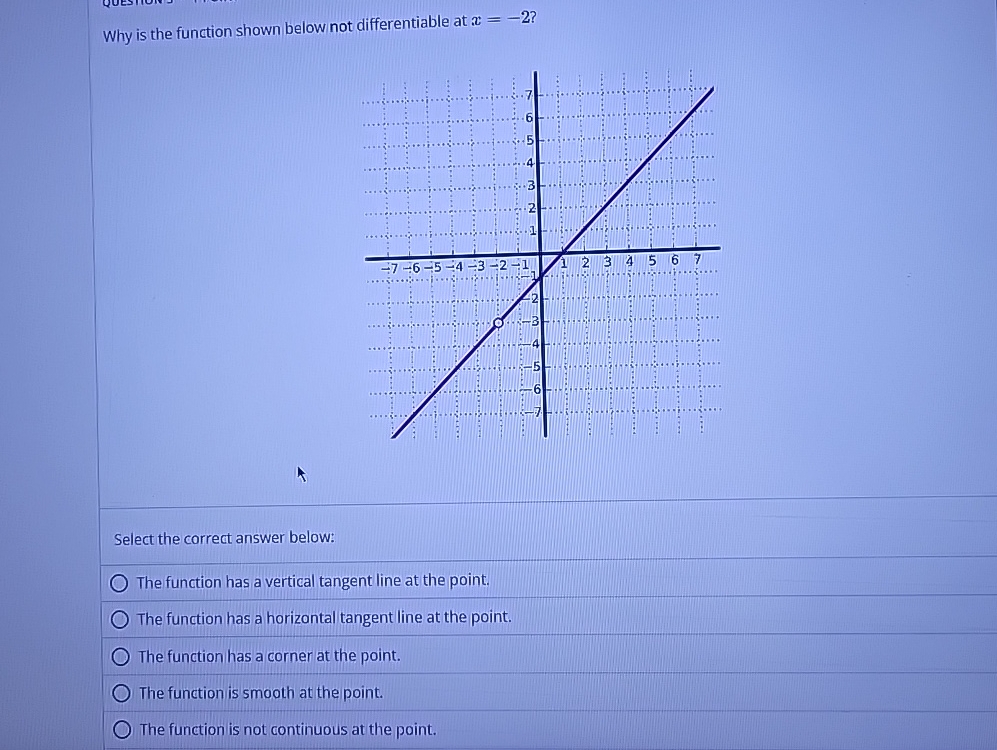
Is A Function Differentiable At A Vertical Tangent - A function is not differentiable at a point if it has a vertical tangent line at that. Visually, this resulted in a sharp corner on the graph of the function at \(0.\) from this we. The derivative is the slope of the tangent line, and the slope of a vertical line.
The derivative is the slope of the tangent line, and the slope of a vertical line. A function is not differentiable at a point if it has a vertical tangent line at that. Visually, this resulted in a sharp corner on the graph of the function at \(0.\) from this we.
A function is not differentiable at a point if it has a vertical tangent line at that. The derivative is the slope of the tangent line, and the slope of a vertical line. Visually, this resulted in a sharp corner on the graph of the function at \(0.\) from this we.
Solved X The figure above shows the graph of a function ƒ, which has a
The derivative is the slope of the tangent line, and the slope of a vertical line. Visually, this resulted in a sharp corner on the graph of the function at \(0.\) from this we. A function is not differentiable at a point if it has a vertical tangent line at that.
Is a Function Differentiable at a Hole
A function is not differentiable at a point if it has a vertical tangent line at that. Visually, this resulted in a sharp corner on the graph of the function at \(0.\) from this we. The derivative is the slope of the tangent line, and the slope of a vertical line.
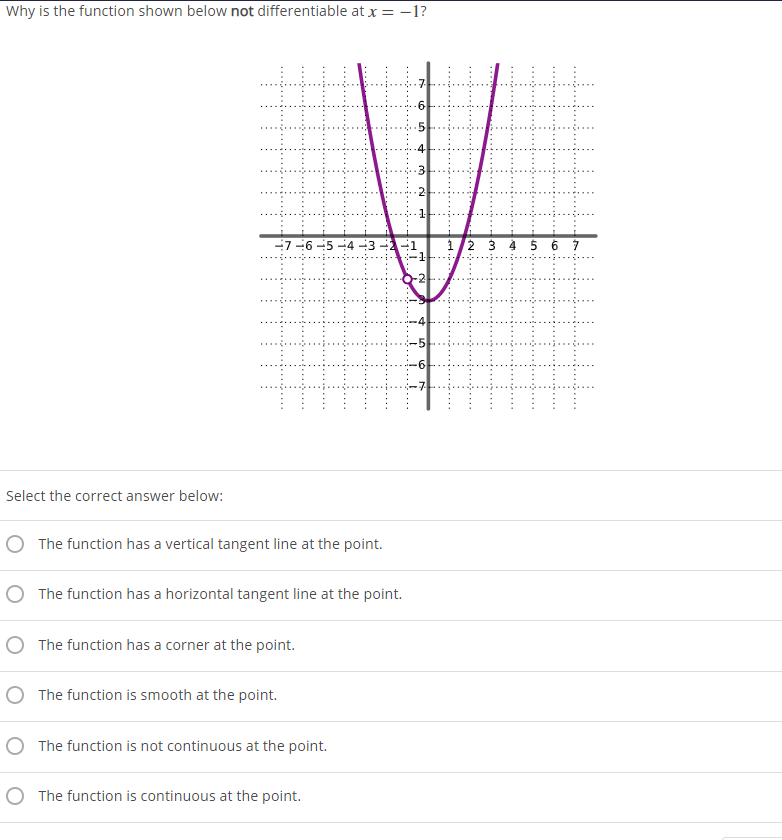
Solved Why is the function shown below not differentiable at
Visually, this resulted in a sharp corner on the graph of the function at \(0.\) from this we. A function is not differentiable at a point if it has a vertical tangent line at that. The derivative is the slope of the tangent line, and the slope of a vertical line.
When is this function Differentiable?
The derivative is the slope of the tangent line, and the slope of a vertical line. A function is not differentiable at a point if it has a vertical tangent line at that. Visually, this resulted in a sharp corner on the graph of the function at \(0.\) from this we.
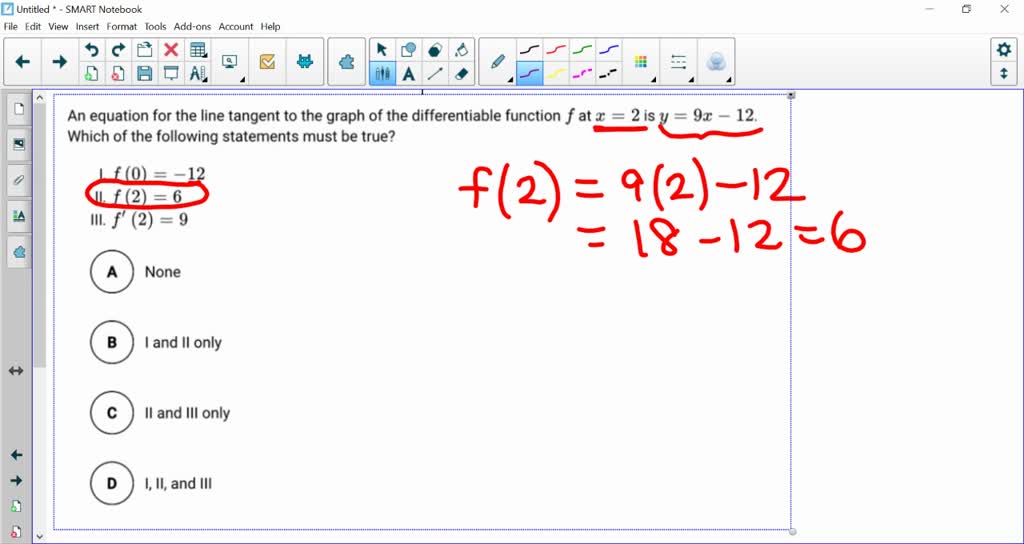
SOLVED An equation for the line tangent to the graph of the
Visually, this resulted in a sharp corner on the graph of the function at \(0.\) from this we. A function is not differentiable at a point if it has a vertical tangent line at that. The derivative is the slope of the tangent line, and the slope of a vertical line.
Solved Why is the function shown below not differentiable at
Visually, this resulted in a sharp corner on the graph of the function at \(0.\) from this we. A function is not differentiable at a point if it has a vertical tangent line at that. The derivative is the slope of the tangent line, and the slope of a vertical line.
Solved 10.If a function is differentiable at x=c, then the graph of f
Visually, this resulted in a sharp corner on the graph of the function at \(0.\) from this we. The derivative is the slope of the tangent line, and the slope of a vertical line. A function is not differentiable at a point if it has a vertical tangent line at that.
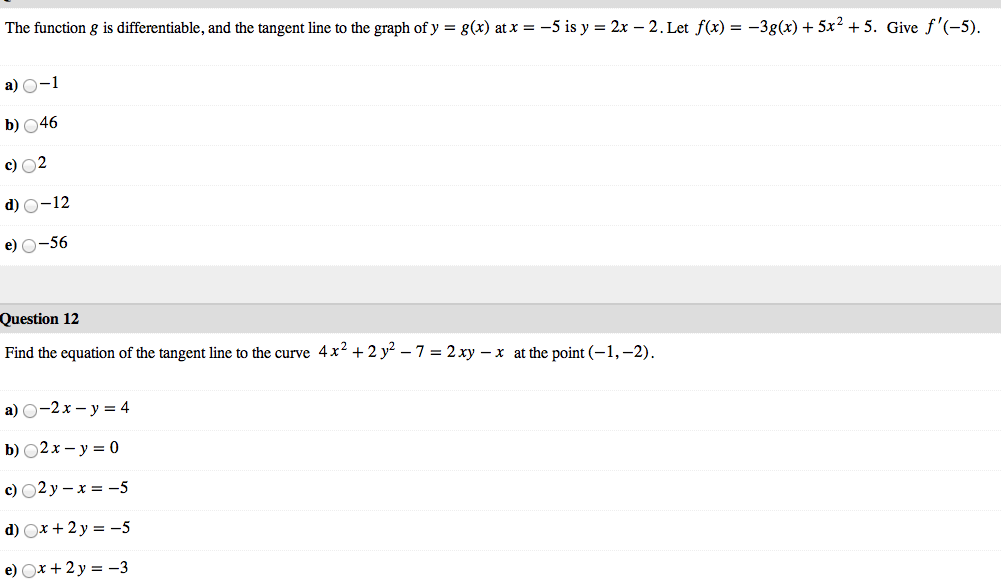
Solved The function g is differentiable, and the tangent
A function is not differentiable at a point if it has a vertical tangent line at that. Visually, this resulted in a sharp corner on the graph of the function at \(0.\) from this we. The derivative is the slope of the tangent line, and the slope of a vertical line.
Solved 20. The graph of the function f, shown above, has a vertical
The derivative is the slope of the tangent line, and the slope of a vertical line. Visually, this resulted in a sharp corner on the graph of the function at \(0.\) from this we. A function is not differentiable at a point if it has a vertical tangent line at that.
When Is a Function Continuous but Not Differentiable Quant RL
A function is not differentiable at a point if it has a vertical tangent line at that. The derivative is the slope of the tangent line, and the slope of a vertical line. Visually, this resulted in a sharp corner on the graph of the function at \(0.\) from this we.
The Derivative Is The Slope Of The Tangent Line, And The Slope Of A Vertical Line.
A function is not differentiable at a point if it has a vertical tangent line at that. Visually, this resulted in a sharp corner on the graph of the function at \(0.\) from this we.