Matrix Calculus Differentiation Neurips - Here, we close this fundamental gap and present an algorithmic framework for computing matrix. Here, we present the first system that performs matrix and tensor calculus automatically. Computing gradients (and hessians) is also an integral part of deep learning frameworks that. Here, we close this fundamental gap and present an algorithmic framework for computing matrix. This course, intended for undergraduates familiar with elementary. Here, we close this fundamental gap and present an algorithmic framework for computing matrix.
Computing gradients (and hessians) is also an integral part of deep learning frameworks that. This course, intended for undergraduates familiar with elementary. Here, we close this fundamental gap and present an algorithmic framework for computing matrix. Here, we present the first system that performs matrix and tensor calculus automatically. Here, we close this fundamental gap and present an algorithmic framework for computing matrix. Here, we close this fundamental gap and present an algorithmic framework for computing matrix.
Here, we close this fundamental gap and present an algorithmic framework for computing matrix. Computing gradients (and hessians) is also an integral part of deep learning frameworks that. This course, intended for undergraduates familiar with elementary. Here, we close this fundamental gap and present an algorithmic framework for computing matrix. Here, we present the first system that performs matrix and tensor calculus automatically. Here, we close this fundamental gap and present an algorithmic framework for computing matrix.
neurips rebuttal
Computing gradients (and hessians) is also an integral part of deep learning frameworks that. Here, we close this fundamental gap and present an algorithmic framework for computing matrix. Here, we close this fundamental gap and present an algorithmic framework for computing matrix. Here, we present the first system that performs matrix and tensor calculus automatically. This course, intended for undergraduates.
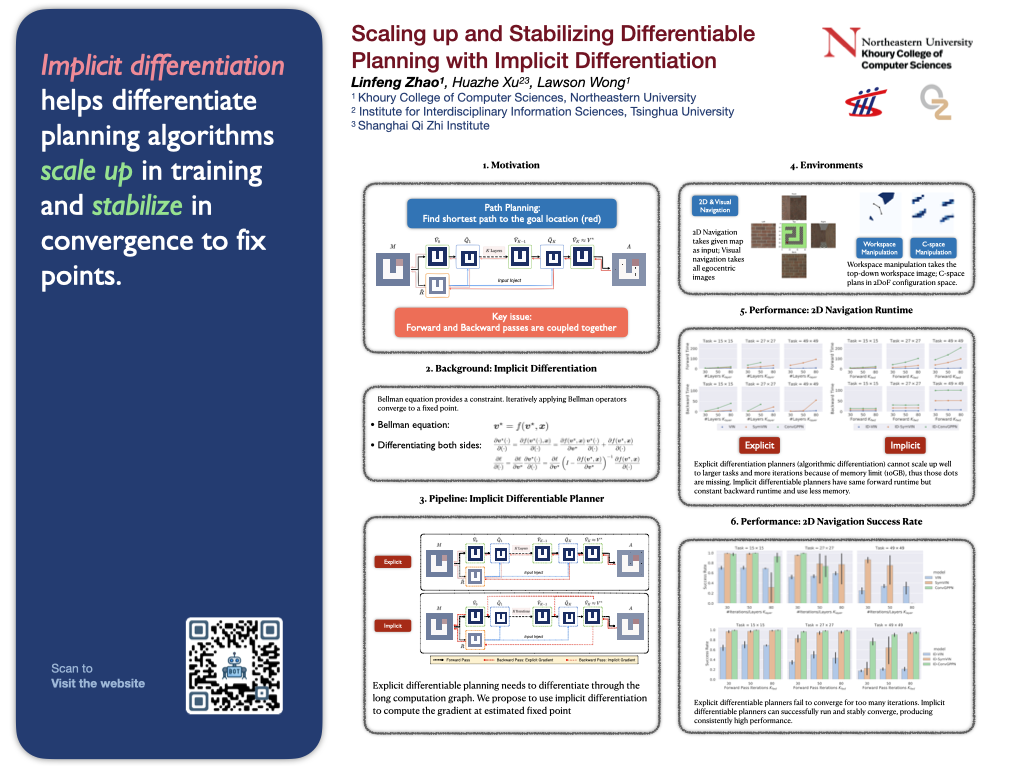
NeurIPS Scaling up and Stabilizing Differentiable Planning with
Computing gradients (and hessians) is also an integral part of deep learning frameworks that. Here, we close this fundamental gap and present an algorithmic framework for computing matrix. This course, intended for undergraduates familiar with elementary. Here, we close this fundamental gap and present an algorithmic framework for computing matrix. Here, we close this fundamental gap and present an algorithmic.
NeurIPS Matrix Estimation for Offline Evaluation in Reinforcement
Here, we present the first system that performs matrix and tensor calculus automatically. Here, we close this fundamental gap and present an algorithmic framework for computing matrix. This course, intended for undergraduates familiar with elementary. Here, we close this fundamental gap and present an algorithmic framework for computing matrix. Here, we close this fundamental gap and present an algorithmic framework.
NeurIPS Misspecification in Inverse Reinforcement Learning
Here, we close this fundamental gap and present an algorithmic framework for computing matrix. Computing gradients (and hessians) is also an integral part of deep learning frameworks that. Here, we close this fundamental gap and present an algorithmic framework for computing matrix. This course, intended for undergraduates familiar with elementary. Here, we present the first system that performs matrix and.
GitHub CNDClab/MatrixCalculus
Here, we close this fundamental gap and present an algorithmic framework for computing matrix. Here, we close this fundamental gap and present an algorithmic framework for computing matrix. Computing gradients (and hessians) is also an integral part of deep learning frameworks that. Here, we present the first system that performs matrix and tensor calculus automatically. This course, intended for undergraduates.
NeurIPS Unleashing the Potential of Fractional Calculus in Graph Neural
Computing gradients (and hessians) is also an integral part of deep learning frameworks that. Here, we close this fundamental gap and present an algorithmic framework for computing matrix. Here, we close this fundamental gap and present an algorithmic framework for computing matrix. This course, intended for undergraduates familiar with elementary. Here, we close this fundamental gap and present an algorithmic.
NeurIPS 2020 What If Neural Networks Had Svds Paper PDF Matrix
Here, we present the first system that performs matrix and tensor calculus automatically. Here, we close this fundamental gap and present an algorithmic framework for computing matrix. Here, we close this fundamental gap and present an algorithmic framework for computing matrix. This course, intended for undergraduates familiar with elementary. Here, we close this fundamental gap and present an algorithmic framework.
NeurIPS Poster Homomorphic Matrix Completion
Here, we close this fundamental gap and present an algorithmic framework for computing matrix. Here, we present the first system that performs matrix and tensor calculus automatically. Here, we close this fundamental gap and present an algorithmic framework for computing matrix. Here, we close this fundamental gap and present an algorithmic framework for computing matrix. Computing gradients (and hessians) is.
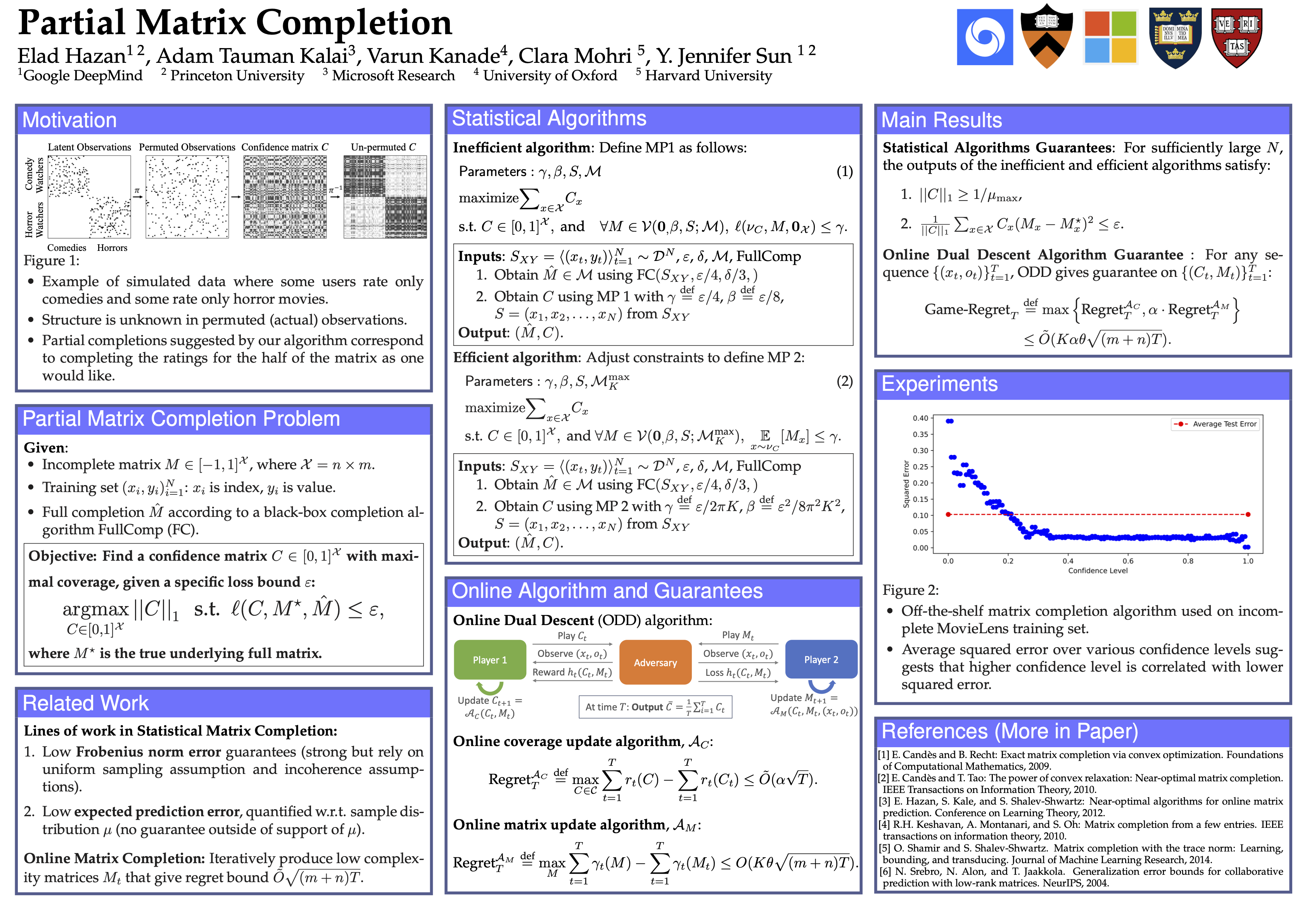
NeurIPS Poster Partial Matrix Completion
Here, we present the first system that performs matrix and tensor calculus automatically. Computing gradients (and hessians) is also an integral part of deep learning frameworks that. Here, we close this fundamental gap and present an algorithmic framework for computing matrix. Here, we close this fundamental gap and present an algorithmic framework for computing matrix. Here, we close this fundamental.
NeurIPS Can Calibration Improve Sample Prioritization?
Here, we close this fundamental gap and present an algorithmic framework for computing matrix. Here, we close this fundamental gap and present an algorithmic framework for computing matrix. Here, we present the first system that performs matrix and tensor calculus automatically. Computing gradients (and hessians) is also an integral part of deep learning frameworks that. Here, we close this fundamental.
Here, We Close This Fundamental Gap And Present An Algorithmic Framework For Computing Matrix.
Computing gradients (and hessians) is also an integral part of deep learning frameworks that. Here, we close this fundamental gap and present an algorithmic framework for computing matrix. Here, we close this fundamental gap and present an algorithmic framework for computing matrix. This course, intended for undergraduates familiar with elementary.