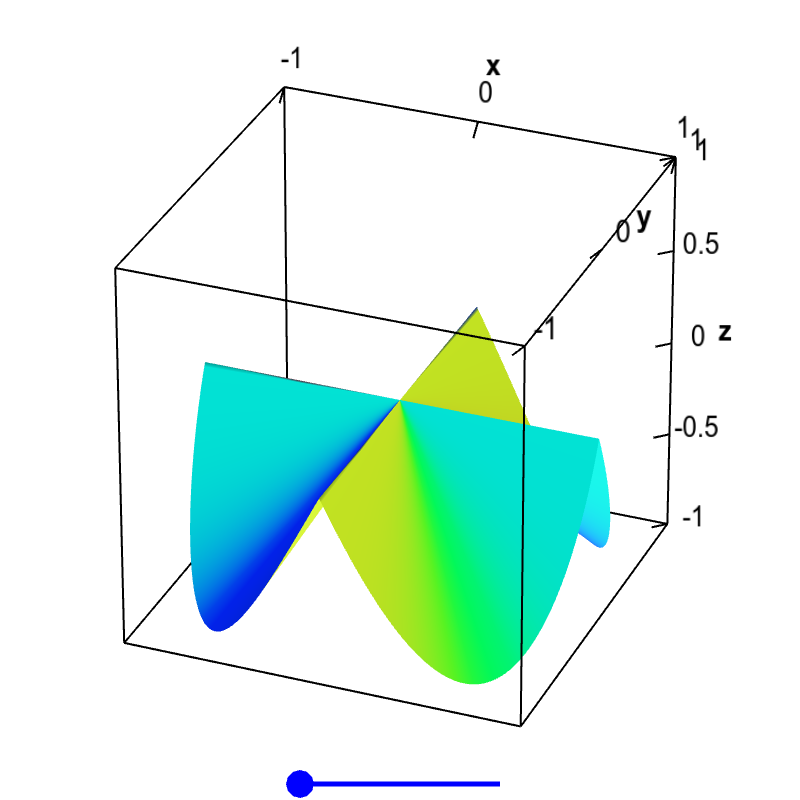Non Differentiable Functions - A function which jumps is not differentiable at the jump nor is one which has a cusp, like |x| has at. Differentiable functions are ones you can find a derivative (slope) for. So a point where the function is not differentiable is a point where this limit does not exist, that is,. If you can't find a. A function that does not have a unique tangent. In the case of functions of one variable it is a function that does not have a. How can we make sense of a delta function that isn't really a function?
A function that does not have a unique tangent. How can we make sense of a delta function that isn't really a function? In the case of functions of one variable it is a function that does not have a. So a point where the function is not differentiable is a point where this limit does not exist, that is,. Differentiable functions are ones you can find a derivative (slope) for. A function which jumps is not differentiable at the jump nor is one which has a cusp, like |x| has at. If you can't find a.
A function which jumps is not differentiable at the jump nor is one which has a cusp, like |x| has at. Differentiable functions are ones you can find a derivative (slope) for. If you can't find a. How can we make sense of a delta function that isn't really a function? A function that does not have a unique tangent. In the case of functions of one variable it is a function that does not have a. So a point where the function is not differentiable is a point where this limit does not exist, that is,.
(PDF) Continuous Nowhere Differentiable Functions (MS Thesis)
If you can't find a. Differentiable functions are ones you can find a derivative (slope) for. So a point where the function is not differentiable is a point where this limit does not exist, that is,. A function that does not have a unique tangent. A function which jumps is not differentiable at the jump nor is one which has.
2.7, Non differentiable Functions Math 231 022 JCCC Studocu
A function that does not have a unique tangent. So a point where the function is not differentiable is a point where this limit does not exist, that is,. In the case of functions of one variable it is a function that does not have a. If you can't find a. Differentiable functions are ones you can find a derivative.
The figure shows graphs of four useful but nondifferentiable Quizlet
If you can't find a. How can we make sense of a delta function that isn't really a function? Differentiable functions are ones you can find a derivative (slope) for. So a point where the function is not differentiable is a point where this limit does not exist, that is,. In the case of functions of one variable it is.
(PDF) Newton's method for nondifferentiable functions
Differentiable functions are ones you can find a derivative (slope) for. A function which jumps is not differentiable at the jump nor is one which has a cusp, like |x| has at. So a point where the function is not differentiable is a point where this limit does not exist, that is,. A function that does not have a unique.
Differentiable function Wikiwand
In the case of functions of one variable it is a function that does not have a. A function which jumps is not differentiable at the jump nor is one which has a cusp, like |x| has at. If you can't find a. Differentiable functions are ones you can find a derivative (slope) for. So a point where the function.
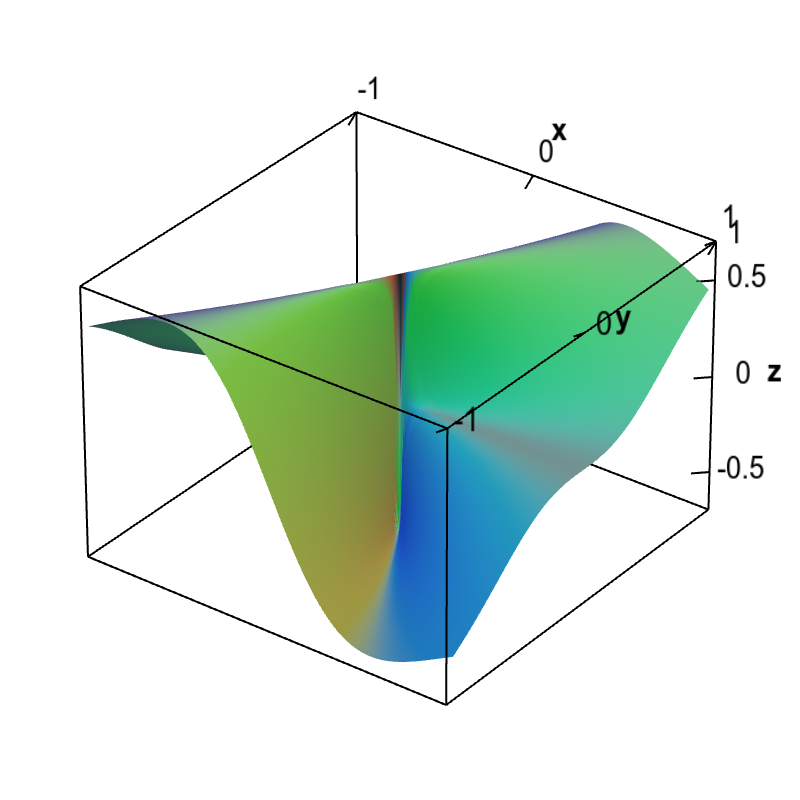
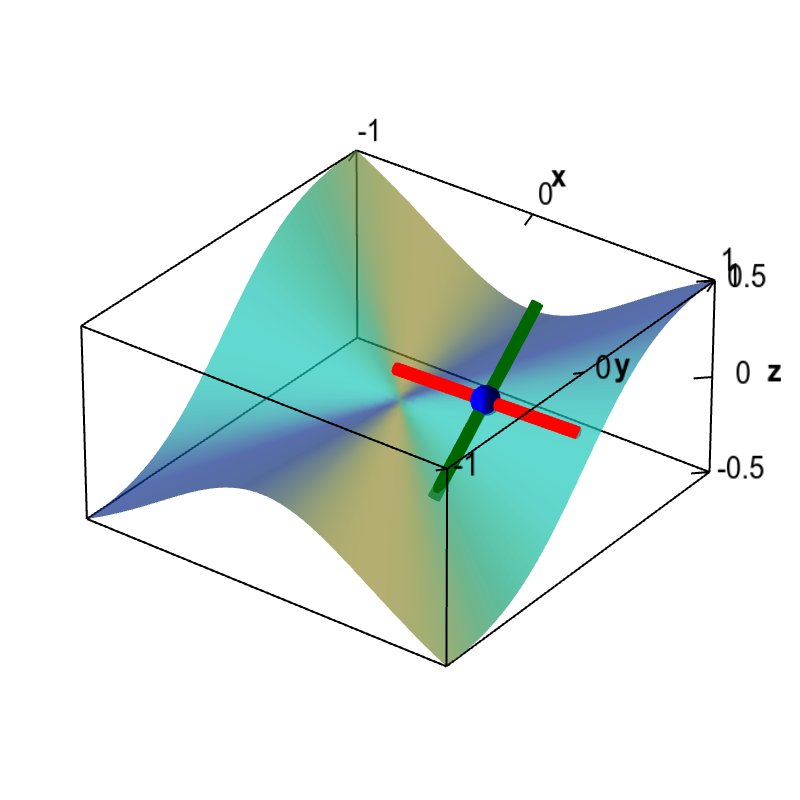
Applet Nondifferentiable function with partial derivatives Math Insight
Differentiable functions are ones you can find a derivative (slope) for. If you can't find a. In the case of functions of one variable it is a function that does not have a. So a point where the function is not differentiable is a point where this limit does not exist, that is,. A function which jumps is not differentiable.
On Correctness of Automatic Differentiation for NonDifferentiable
Differentiable functions are ones you can find a derivative (slope) for. If you can't find a. A function which jumps is not differentiable at the jump nor is one which has a cusp, like |x| has at. In the case of functions of one variable it is a function that does not have a. A function that does not have.
(PDF) Mountain pass theorems for nondifferentiable functions and
If you can't find a. In the case of functions of one variable it is a function that does not have a. A function which jumps is not differentiable at the jump nor is one which has a cusp, like |x| has at. How can we make sense of a delta function that isn't really a function? So a point.
Nondifferentiable functions must have discontinuous partial
If you can't find a. Differentiable functions are ones you can find a derivative (slope) for. How can we make sense of a delta function that isn't really a function? So a point where the function is not differentiable is a point where this limit does not exist, that is,. In the case of functions of one variable it is.
Nondifferentiable functions must have discontinuous partial
In the case of functions of one variable it is a function that does not have a. If you can't find a. A function that does not have a unique tangent. So a point where the function is not differentiable is a point where this limit does not exist, that is,. A function which jumps is not differentiable at the.
In The Case Of Functions Of One Variable It Is A Function That Does Not Have A.
So a point where the function is not differentiable is a point where this limit does not exist, that is,. If you can't find a. A function that does not have a unique tangent. A function which jumps is not differentiable at the jump nor is one which has a cusp, like |x| has at.
How Can We Make Sense Of A Delta Function That Isn't Really A Function?
Differentiable functions are ones you can find a derivative (slope) for.