Phase Portrait Differential Equations - Would like to understand how the eigenvalues for a system of two differential equations can determine the type of phase portrait attained by. If 0 <d<t2=4, the eigenvalues are real, distinct, and of the same sign, and the phase. Phase portrait is a saddle (which is always unstable). The phase portrait is a graphical tool to visualize how the solutions of a given system of diferential equations behaves in the long run. Learn how to sketch trajectories and phase portraits for homogeneous systems of differential equations in the x1x2 plane. Learn how to draw and interpret phase portraits of two dimensional linear systems, using eigenvalues and eigenvectors. 1 > 2 > 0 nodal. Classification of 2d systems distinct real eigenvalues. 1 > 0 > 2.
The phase portrait is a graphical tool to visualize how the solutions of a given system of diferential equations behaves in the long run. Phase portrait is a saddle (which is always unstable). 1 > 2 > 0 nodal. 1 > 0 > 2. Learn how to draw and interpret phase portraits of two dimensional linear systems, using eigenvalues and eigenvectors. If 0 <d<t2=4, the eigenvalues are real, distinct, and of the same sign, and the phase. Would like to understand how the eigenvalues for a system of two differential equations can determine the type of phase portrait attained by. Learn how to sketch trajectories and phase portraits for homogeneous systems of differential equations in the x1x2 plane. Classification of 2d systems distinct real eigenvalues.
Classification of 2d systems distinct real eigenvalues. Would like to understand how the eigenvalues for a system of two differential equations can determine the type of phase portrait attained by. Phase portrait is a saddle (which is always unstable). Learn how to sketch trajectories and phase portraits for homogeneous systems of differential equations in the x1x2 plane. If 0 <d<t2=4, the eigenvalues are real, distinct, and of the same sign, and the phase. 1 > 2 > 0 nodal. 1 > 0 > 2. The phase portrait is a graphical tool to visualize how the solutions of a given system of diferential equations behaves in the long run. Learn how to draw and interpret phase portraits of two dimensional linear systems, using eigenvalues and eigenvectors.
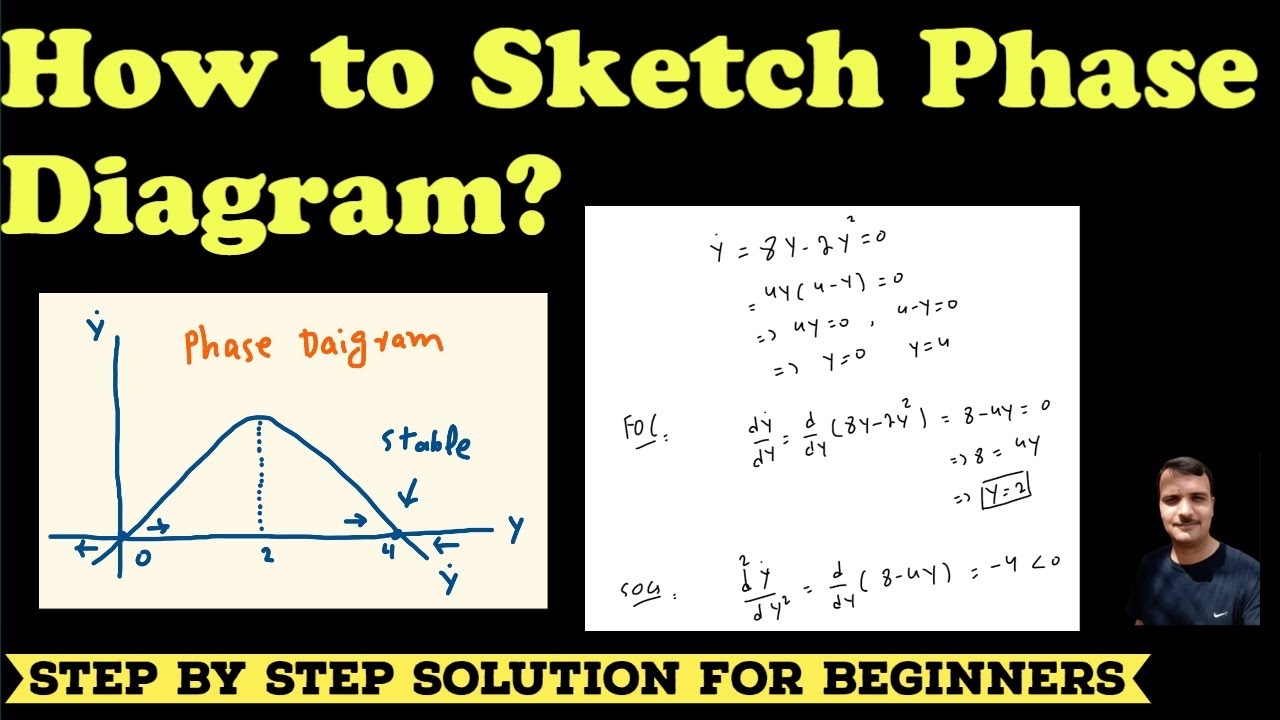
Differential Equations Phase Diagram
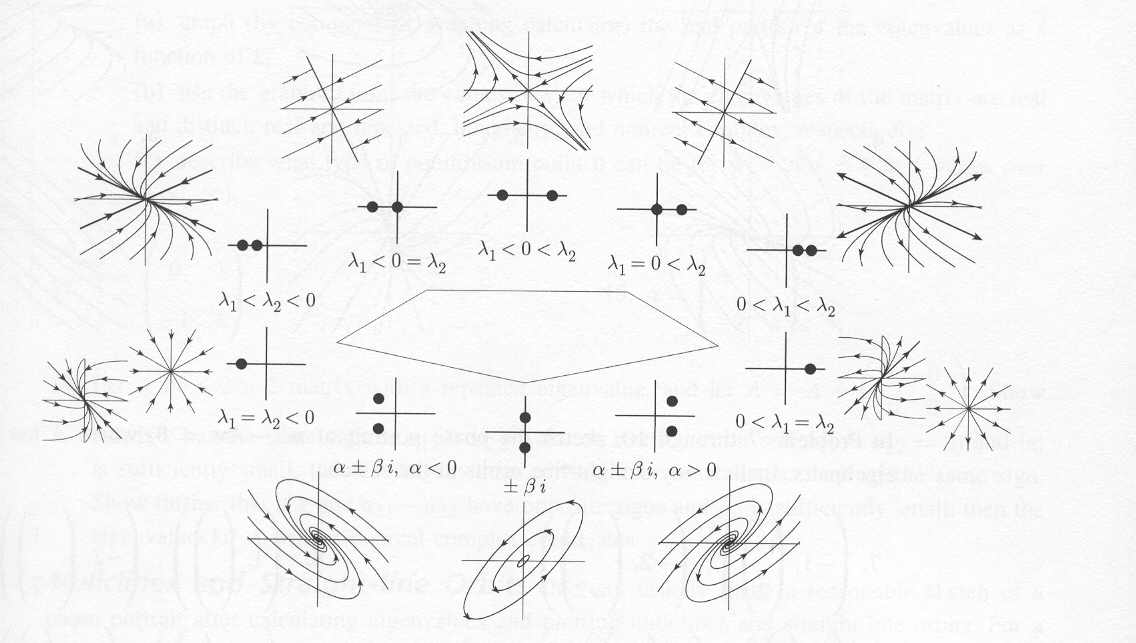
Classification of 2d systems distinct real eigenvalues. Learn how to draw and interpret phase portraits of two dimensional linear systems, using eigenvalues and eigenvectors. Would like to understand how the eigenvalues for a system of two differential equations can determine the type of phase portrait attained by. 1 > 2 > 0 nodal. If 0 <d<t2=4, the eigenvalues are real,.
Phase portrait for the system of differential equations for E = 0.417
Classification of 2d systems distinct real eigenvalues. If 0 <d<t2=4, the eigenvalues are real, distinct, and of the same sign, and the phase. Learn how to draw and interpret phase portraits of two dimensional linear systems, using eigenvalues and eigenvectors. 1 > 0 > 2. The phase portrait is a graphical tool to visualize how the solutions of a given.
System of differential equations, phase portraits and stability of
1 > 2 > 0 nodal. If 0 <d<t2=4, the eigenvalues are real, distinct, and of the same sign, and the phase. Would like to understand how the eigenvalues for a system of two differential equations can determine the type of phase portrait attained by. The phase portrait is a graphical tool to visualize how the solutions of a given.
(Phase Portrait) Analysis A Visual Approach
1 > 0 > 2. Classification of 2d systems distinct real eigenvalues. The phase portrait is a graphical tool to visualize how the solutions of a given system of diferential equations behaves in the long run. Learn how to draw and interpret phase portraits of two dimensional linear systems, using eigenvalues and eigenvectors. Would like to understand how the eigenvalues.
Phase Diagram Straight Line Solutions Differential Equations
1 > 2 > 0 nodal. Phase portrait is a saddle (which is always unstable). The phase portrait is a graphical tool to visualize how the solutions of a given system of diferential equations behaves in the long run. Learn how to draw and interpret phase portraits of two dimensional linear systems, using eigenvalues and eigenvectors. Classification of 2d systems.
Differential Equations Phase Diagram
1 > 2 > 0 nodal. 1 > 0 > 2. Phase portrait is a saddle (which is always unstable). The phase portrait is a graphical tool to visualize how the solutions of a given system of diferential equations behaves in the long run. Learn how to sketch trajectories and phase portraits for homogeneous systems of differential equations in the.
Providing initial conditions for differential equation? Phase
Learn how to sketch trajectories and phase portraits for homogeneous systems of differential equations in the x1x2 plane. The phase portrait is a graphical tool to visualize how the solutions of a given system of diferential equations behaves in the long run. 1 > 2 > 0 nodal. Learn how to draw and interpret phase portraits of two dimensional linear.
differential equations
Would like to understand how the eigenvalues for a system of two differential equations can determine the type of phase portrait attained by. Classification of 2d systems distinct real eigenvalues. 1 > 0 > 2. 1 > 2 > 0 nodal. Phase portrait is a saddle (which is always unstable).
How does my phase portrait fit with my differential equation
If 0 <d<t2=4, the eigenvalues are real, distinct, and of the same sign, and the phase. The phase portrait is a graphical tool to visualize how the solutions of a given system of diferential equations behaves in the long run. Phase portrait is a saddle (which is always unstable). Learn how to draw and interpret phase portraits of two dimensional.
tikz pgf Drawing the phase portrait of two differential equations
1 > 0 > 2. Classification of 2d systems distinct real eigenvalues. Would like to understand how the eigenvalues for a system of two differential equations can determine the type of phase portrait attained by. The phase portrait is a graphical tool to visualize how the solutions of a given system of diferential equations behaves in the long run. 1.
Classification Of 2D Systems Distinct Real Eigenvalues.
If 0 <d<t2=4, the eigenvalues are real, distinct, and of the same sign, and the phase. The phase portrait is a graphical tool to visualize how the solutions of a given system of diferential equations behaves in the long run. Learn how to sketch trajectories and phase portraits for homogeneous systems of differential equations in the x1x2 plane. Learn how to draw and interpret phase portraits of two dimensional linear systems, using eigenvalues and eigenvectors.
Would Like To Understand How The Eigenvalues For A System Of Two Differential Equations Can Determine The Type Of Phase Portrait Attained By.
Phase portrait is a saddle (which is always unstable). 1 > 0 > 2. 1 > 2 > 0 nodal.