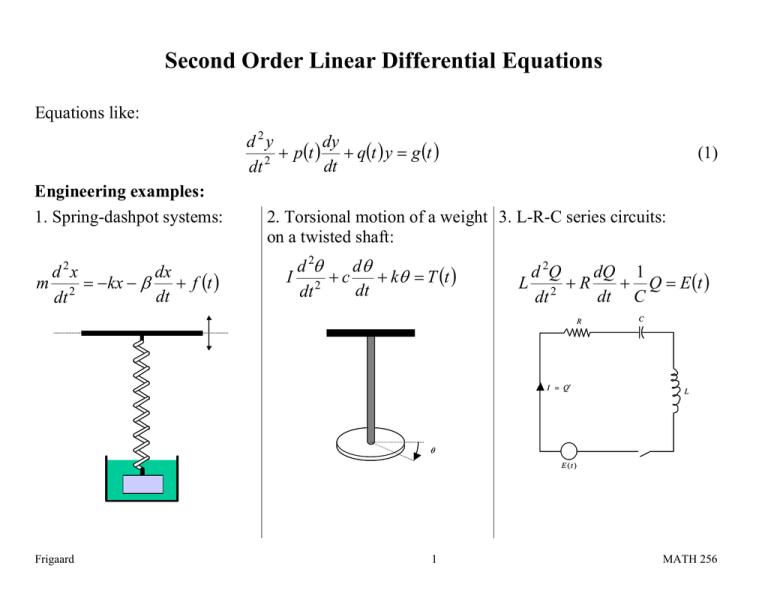
Solving Second Order Linear Differential Equations - Those that are linear and have constant. It is crucial in many areas of physics. Generally, we write a second order differential equation as y'' + p (x)y' + q (x)y = f (x), where p (x), q (x), and f (x) are functions of x. In this section we start to learn how to solve second order differential equations of a particular type: But it is always possible to do so if the coefficient.
In this section we start to learn how to solve second order differential equations of a particular type: Those that are linear and have constant. But it is always possible to do so if the coefficient. It is crucial in many areas of physics. Generally, we write a second order differential equation as y'' + p (x)y' + q (x)y = f (x), where p (x), q (x), and f (x) are functions of x.
Those that are linear and have constant. But it is always possible to do so if the coefficient. In this section we start to learn how to solve second order differential equations of a particular type: Generally, we write a second order differential equation as y'' + p (x)y' + q (x)y = f (x), where p (x), q (x), and f (x) are functions of x. It is crucial in many areas of physics.
Chapter 8 Solving Second order differential equations numerically
In this section we start to learn how to solve second order differential equations of a particular type: Those that are linear and have constant. It is crucial in many areas of physics. Generally, we write a second order differential equation as y'' + p (x)y' + q (x)y = f (x), where p (x), q (x), and f (x).
(PDF) Second Order Differential Equations
Those that are linear and have constant. But it is always possible to do so if the coefficient. In this section we start to learn how to solve second order differential equations of a particular type: It is crucial in many areas of physics. Generally, we write a second order differential equation as y'' + p (x)y' + q (x)y.
PPT First Order Linear Differential Equations PowerPoint Presentation
Generally, we write a second order differential equation as y'' + p (x)y' + q (x)y = f (x), where p (x), q (x), and f (x) are functions of x. In this section we start to learn how to solve second order differential equations of a particular type: It is crucial in many areas of physics. But it is.
(PDF) Solving third order linear differential equations in terms of
Generally, we write a second order differential equation as y'' + p (x)y' + q (x)y = f (x), where p (x), q (x), and f (x) are functions of x. But it is always possible to do so if the coefficient. It is crucial in many areas of physics. Those that are linear and have constant. In this section.
Solved Solve the following second order linear differential
Generally, we write a second order differential equation as y'' + p (x)y' + q (x)y = f (x), where p (x), q (x), and f (x) are functions of x. Those that are linear and have constant. But it is always possible to do so if the coefficient. In this section we start to learn how to solve second.
Second Order Linear Differential Equations ( )
It is crucial in many areas of physics. Generally, we write a second order differential equation as y'' + p (x)y' + q (x)y = f (x), where p (x), q (x), and f (x) are functions of x. But it is always possible to do so if the coefficient. In this section we start to learn how to solve.
Solved Exercise 3 Solve the following second order linear
In this section we start to learn how to solve second order differential equations of a particular type: It is crucial in many areas of physics. Generally, we write a second order differential equation as y'' + p (x)y' + q (x)y = f (x), where p (x), q (x), and f (x) are functions of x. But it is.
SecondOrder Linear Differential Equations
Generally, we write a second order differential equation as y'' + p (x)y' + q (x)y = f (x), where p (x), q (x), and f (x) are functions of x. But it is always possible to do so if the coefficient. Those that are linear and have constant. It is crucial in many areas of physics. In this section.
Second Order Linear Differential Equations
Generally, we write a second order differential equation as y'' + p (x)y' + q (x)y = f (x), where p (x), q (x), and f (x) are functions of x. But it is always possible to do so if the coefficient. It is crucial in many areas of physics. Those that are linear and have constant. In this section.
Solving secondorder differential equations. Mathematics Stack Exchange
Generally, we write a second order differential equation as y'' + p (x)y' + q (x)y = f (x), where p (x), q (x), and f (x) are functions of x. It is crucial in many areas of physics. In this section we start to learn how to solve second order differential equations of a particular type: Those that are.
It Is Crucial In Many Areas Of Physics.
Those that are linear and have constant. In this section we start to learn how to solve second order differential equations of a particular type: Generally, we write a second order differential equation as y'' + p (x)y' + q (x)y = f (x), where p (x), q (x), and f (x) are functions of x. But it is always possible to do so if the coefficient.