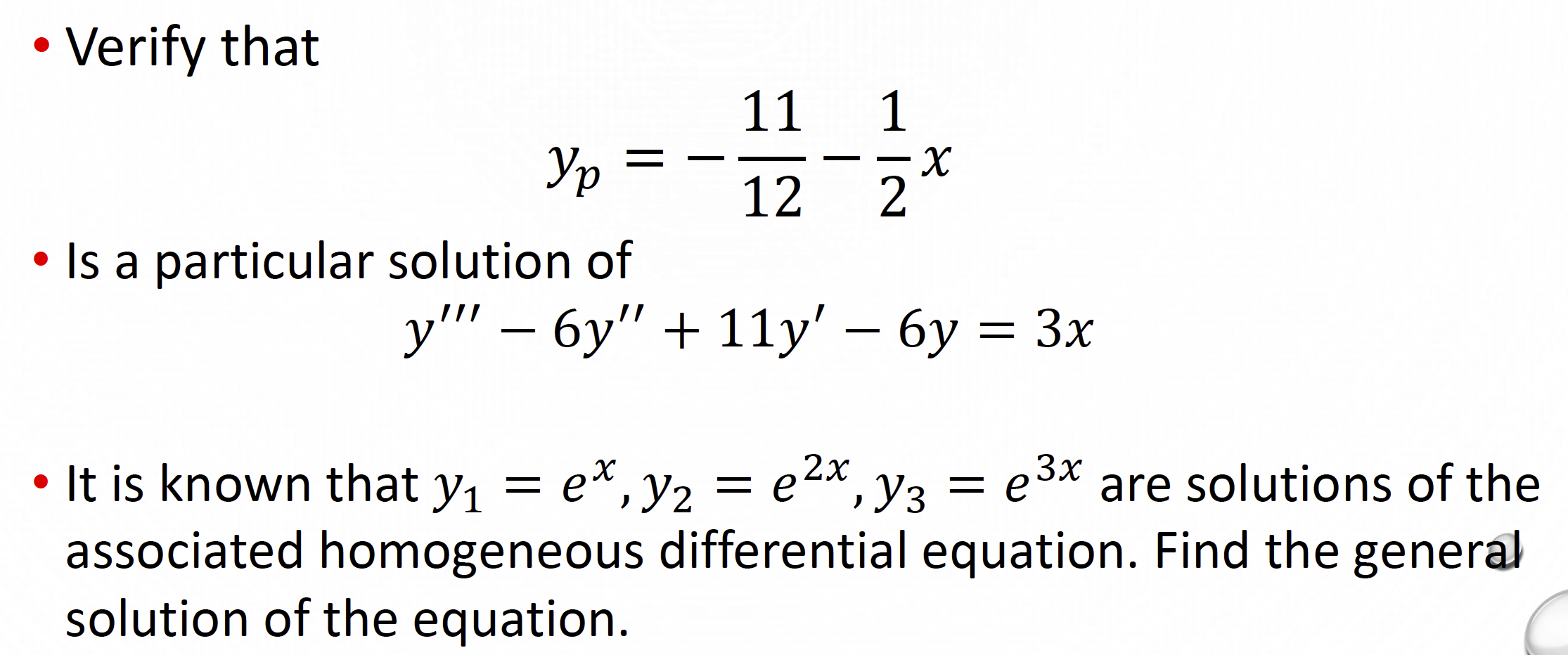Superposition Differential Equations - To prove this, we compute. + 2x = 1 + e−2t solution. The principle of superposition states that \(x = x(t)\) is also a solution of \(\eqref{eq:1}\). Suppose that we have a linear homogenous second order differential equation $\frac{d^2 y}{dt^2} + p(t). We consider a linear combination of x1 and x2 by letting. We saw the principle of superposition already, for first order equations. In this section give an in depth discussion on the process used to solve homogeneous, linear, second order differential. Use superposition to find a solution to x. X(t) = c1x1(t) +c2x2(t), with c1 and c2 constants. For example, we saw that if y1 is a solution to y + 4y = sin(3t) and y2 a.
Use superposition to find a solution to x. Suppose that we have a linear homogenous second order differential equation $\frac{d^2 y}{dt^2} + p(t). In this section give an in depth discussion on the process used to solve homogeneous, linear, second order differential. We saw the principle of superposition already, for first order equations. X(t) = c1x1(t) +c2x2(t), with c1 and c2 constants. For example, we saw that if y1 is a solution to y + 4y = sin(3t) and y2 a. We consider a linear combination of x1 and x2 by letting. To prove this, we compute. The principle of superposition states that \(x = x(t)\) is also a solution of \(\eqref{eq:1}\). The input is a superposition of the inputs from (i) and (ii).
The principle of superposition states that \(x = x(t)\) is also a solution of \(\eqref{eq:1}\). For example, we saw that if y1 is a solution to y + 4y = sin(3t) and y2 a. We saw the principle of superposition already, for first order equations. In this section give an in depth discussion on the process used to solve homogeneous, linear, second order differential. We consider a linear combination of x1 and x2 by letting. The input is a superposition of the inputs from (i) and (ii). Suppose that we have a linear homogenous second order differential equation $\frac{d^2 y}{dt^2} + p(t). Use superposition to find a solution to x. X(t) = c1x1(t) +c2x2(t), with c1 and c2 constants. + 2x = 1 + e−2t solution.
Differential Equations Undetermined Coefficients Superposition
Suppose that we have a linear homogenous second order differential equation $\frac{d^2 y}{dt^2} + p(t). To prove this, we compute. In this section give an in depth discussion on the process used to solve homogeneous, linear, second order differential. For example, we saw that if y1 is a solution to y + 4y = sin(3t) and y2 a. The principle.
Superposition Principle (and Undetermined Coefficients revisited
Use superposition to find a solution to x. We consider a linear combination of x1 and x2 by letting. + 2x = 1 + e−2t solution. The principle of superposition states that \(x = x(t)\) is also a solution of \(\eqref{eq:1}\). Suppose that we have a linear homogenous second order differential equation $\frac{d^2 y}{dt^2} + p(t).
ordinary differential equations Principle of superposition
The principle of superposition states that \(x = x(t)\) is also a solution of \(\eqref{eq:1}\). + 2x = 1 + e−2t solution. In this section give an in depth discussion on the process used to solve homogeneous, linear, second order differential. For example, we saw that if y1 is a solution to y + 4y = sin(3t) and y2 a..
Solved Differential Equations Superposition principle
In this section give an in depth discussion on the process used to solve homogeneous, linear, second order differential. Suppose that we have a linear homogenous second order differential equation $\frac{d^2 y}{dt^2} + p(t). We saw the principle of superposition already, for first order equations. The principle of superposition states that \(x = x(t)\) is also a solution of \(\eqref{eq:1}\)..
PPT HigherOrder Differential Equations PowerPoint Presentation, free
Suppose that we have a linear homogenous second order differential equation $\frac{d^2 y}{dt^2} + p(t). Use superposition to find a solution to x. The principle of superposition states that \(x = x(t)\) is also a solution of \(\eqref{eq:1}\). + 2x = 1 + e−2t solution. We saw the principle of superposition already, for first order equations.
Diff Eqn Verify the Principle of Superposition YouTube
+ 2x = 1 + e−2t solution. The input is a superposition of the inputs from (i) and (ii). The principle of superposition states that \(x = x(t)\) is also a solution of \(\eqref{eq:1}\). X(t) = c1x1(t) +c2x2(t), with c1 and c2 constants. Suppose that we have a linear homogenous second order differential equation $\frac{d^2 y}{dt^2} + p(t).
Superposition for linear differential equations YouTube
Suppose that we have a linear homogenous second order differential equation $\frac{d^2 y}{dt^2} + p(t). To prove this, we compute. The input is a superposition of the inputs from (i) and (ii). For example, we saw that if y1 is a solution to y + 4y = sin(3t) and y2 a. X(t) = c1x1(t) +c2x2(t), with c1 and c2 constants.
Lesson 26Superposition Undetermined Coefficients to Solve Non
+ 2x = 1 + e−2t solution. Suppose that we have a linear homogenous second order differential equation $\frac{d^2 y}{dt^2} + p(t). Use superposition to find a solution to x. We consider a linear combination of x1 and x2 by letting. To prove this, we compute.
PPT Chapter 4 HigherOrder Differential Equations PowerPoint
For example, we saw that if y1 is a solution to y + 4y = sin(3t) and y2 a. The input is a superposition of the inputs from (i) and (ii). X(t) = c1x1(t) +c2x2(t), with c1 and c2 constants. + 2x = 1 + e−2t solution. We saw the principle of superposition already, for first order equations.
Table 1 from A splitting technique for superposition type solutions of
To prove this, we compute. We consider a linear combination of x1 and x2 by letting. X(t) = c1x1(t) +c2x2(t), with c1 and c2 constants. In this section give an in depth discussion on the process used to solve homogeneous, linear, second order differential. + 2x = 1 + e−2t solution.
+ 2X = 1 + E−2T Solution.
Suppose that we have a linear homogenous second order differential equation $\frac{d^2 y}{dt^2} + p(t). For example, we saw that if y1 is a solution to y + 4y = sin(3t) and y2 a. We consider a linear combination of x1 and x2 by letting. The principle of superposition states that \(x = x(t)\) is also a solution of \(\eqref{eq:1}\).
To Prove This, We Compute.
We saw the principle of superposition already, for first order equations. Use superposition to find a solution to x. In this section give an in depth discussion on the process used to solve homogeneous, linear, second order differential. The input is a superposition of the inputs from (i) and (ii).