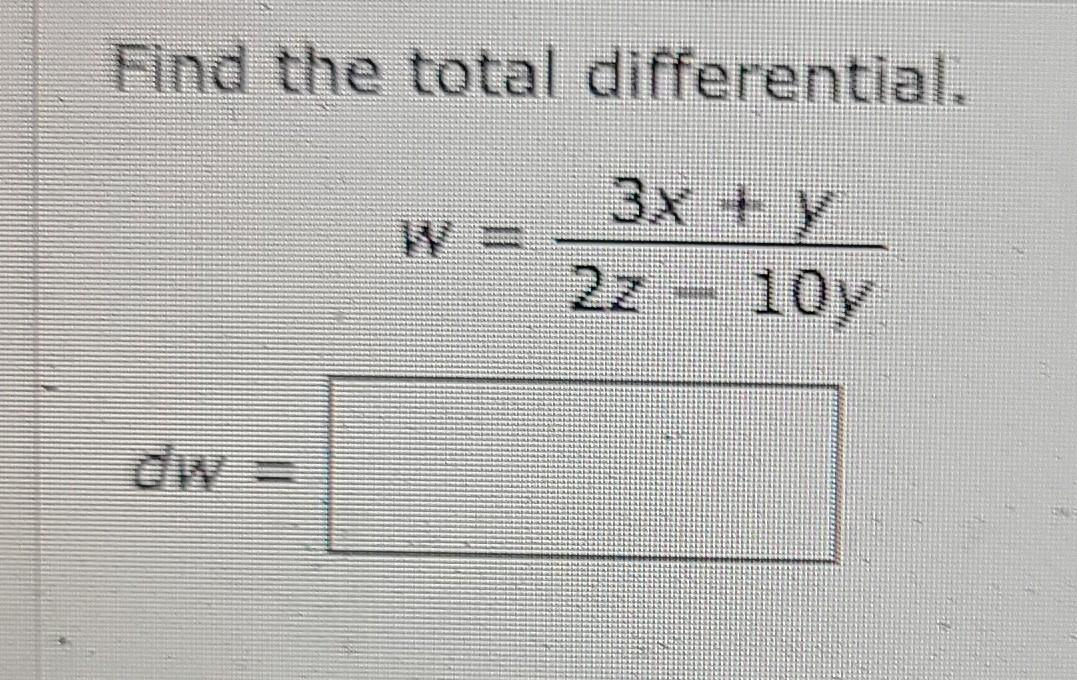Total Differential Formula - Let \(dx\), \(dy\) and \(dz\) represent changes. Learn how to compute the total differential of a function of several variables using the chain rule and the tangent approximation formula. For a function of two or more independent variables, the total differential of the function is the sum over all of the independent variables of. Let \(w=f(x,y,z)\) be continuous on an open set \(s\).
Learn how to compute the total differential of a function of several variables using the chain rule and the tangent approximation formula. Let \(w=f(x,y,z)\) be continuous on an open set \(s\). For a function of two or more independent variables, the total differential of the function is the sum over all of the independent variables of. Let \(dx\), \(dy\) and \(dz\) represent changes.
For a function of two or more independent variables, the total differential of the function is the sum over all of the independent variables of. Let \(w=f(x,y,z)\) be continuous on an open set \(s\). Let \(dx\), \(dy\) and \(dz\) represent changes. Learn how to compute the total differential of a function of several variables using the chain rule and the tangent approximation formula.
Exact differential equations Yawin
Let \(w=f(x,y,z)\) be continuous on an open set \(s\). Learn how to compute the total differential of a function of several variables using the chain rule and the tangent approximation formula. Let \(dx\), \(dy\) and \(dz\) represent changes. For a function of two or more independent variables, the total differential of the function is the sum over all of the.
Exact differential equation Alchetron, the free social encyclopedia
For a function of two or more independent variables, the total differential of the function is the sum over all of the independent variables of. Let \(w=f(x,y,z)\) be continuous on an open set \(s\). Let \(dx\), \(dy\) and \(dz\) represent changes. Learn how to compute the total differential of a function of several variables using the chain rule and the.
SOLUTION 3 6 the total differential Studypool
Let \(w=f(x,y,z)\) be continuous on an open set \(s\). Let \(dx\), \(dy\) and \(dz\) represent changes. Learn how to compute the total differential of a function of several variables using the chain rule and the tangent approximation formula. For a function of two or more independent variables, the total differential of the function is the sum over all of the.
partial derivative Total differential definition help Mathematics
Learn how to compute the total differential of a function of several variables using the chain rule and the tangent approximation formula. Let \(dx\), \(dy\) and \(dz\) represent changes. Let \(w=f(x,y,z)\) be continuous on an open set \(s\). For a function of two or more independent variables, the total differential of the function is the sum over all of the.
Differential Expansion Formula at Laura Malone blog
For a function of two or more independent variables, the total differential of the function is the sum over all of the independent variables of. Let \(w=f(x,y,z)\) be continuous on an open set \(s\). Learn how to compute the total differential of a function of several variables using the chain rule and the tangent approximation formula. Let \(dx\), \(dy\) and.
⏩SOLVEDWrite a differential formula that estimates the given change
Let \(w=f(x,y,z)\) be continuous on an open set \(s\). For a function of two or more independent variables, the total differential of the function is the sum over all of the independent variables of. Let \(dx\), \(dy\) and \(dz\) represent changes. Learn how to compute the total differential of a function of several variables using the chain rule and the.
Differential Calculus (Formulas and Examples)
Let \(w=f(x,y,z)\) be continuous on an open set \(s\). Let \(dx\), \(dy\) and \(dz\) represent changes. For a function of two or more independent variables, the total differential of the function is the sum over all of the independent variables of. Learn how to compute the total differential of a function of several variables using the chain rule and the.
Differential Equation Meaning, Types, Order, Degree & Solution Cuemath
Learn how to compute the total differential of a function of several variables using the chain rule and the tangent approximation formula. Let \(w=f(x,y,z)\) be continuous on an open set \(s\). Let \(dx\), \(dy\) and \(dz\) represent changes. For a function of two or more independent variables, the total differential of the function is the sum over all of the.
calculus Visualizing the total differential Mathematics Stack Exchange
Let \(dx\), \(dy\) and \(dz\) represent changes. Let \(w=f(x,y,z)\) be continuous on an open set \(s\). Learn how to compute the total differential of a function of several variables using the chain rule and the tangent approximation formula. For a function of two or more independent variables, the total differential of the function is the sum over all of the.
Solved Find the total differential. 3х + у 10y
Learn how to compute the total differential of a function of several variables using the chain rule and the tangent approximation formula. Let \(dx\), \(dy\) and \(dz\) represent changes. Let \(w=f(x,y,z)\) be continuous on an open set \(s\). For a function of two or more independent variables, the total differential of the function is the sum over all of the.
For A Function Of Two Or More Independent Variables, The Total Differential Of The Function Is The Sum Over All Of The Independent Variables Of.
Let \(w=f(x,y,z)\) be continuous on an open set \(s\). Let \(dx\), \(dy\) and \(dz\) represent changes. Learn how to compute the total differential of a function of several variables using the chain rule and the tangent approximation formula.