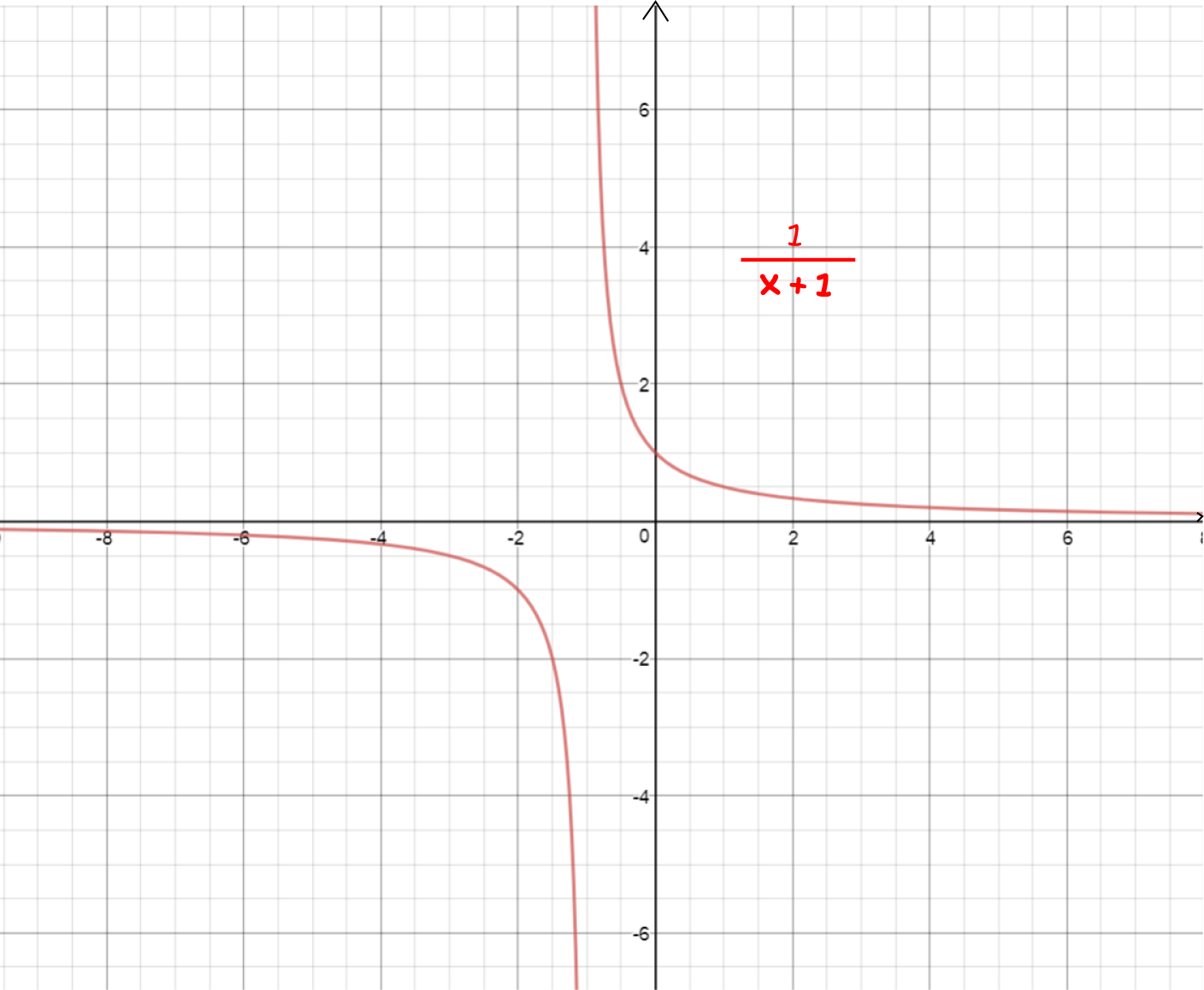
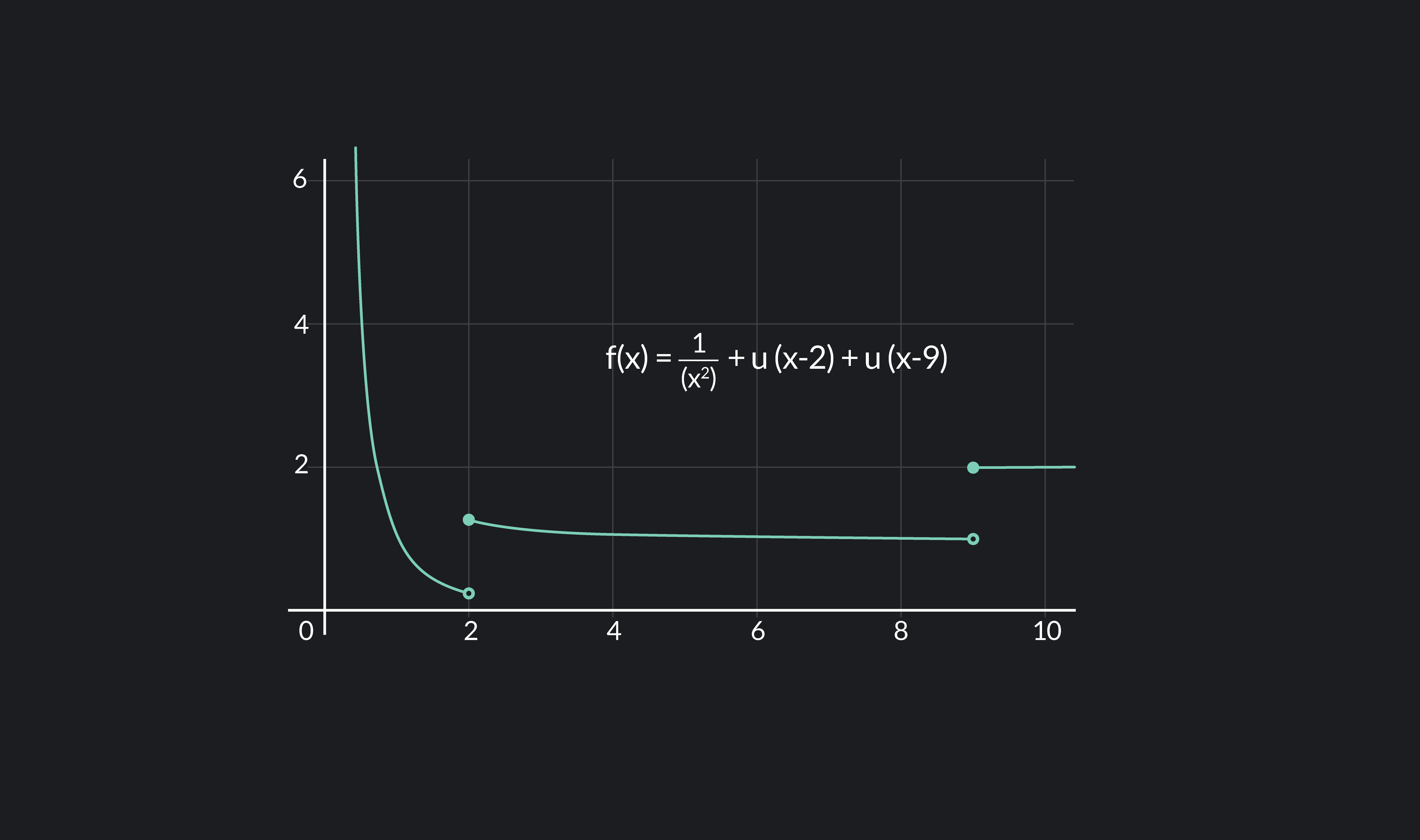
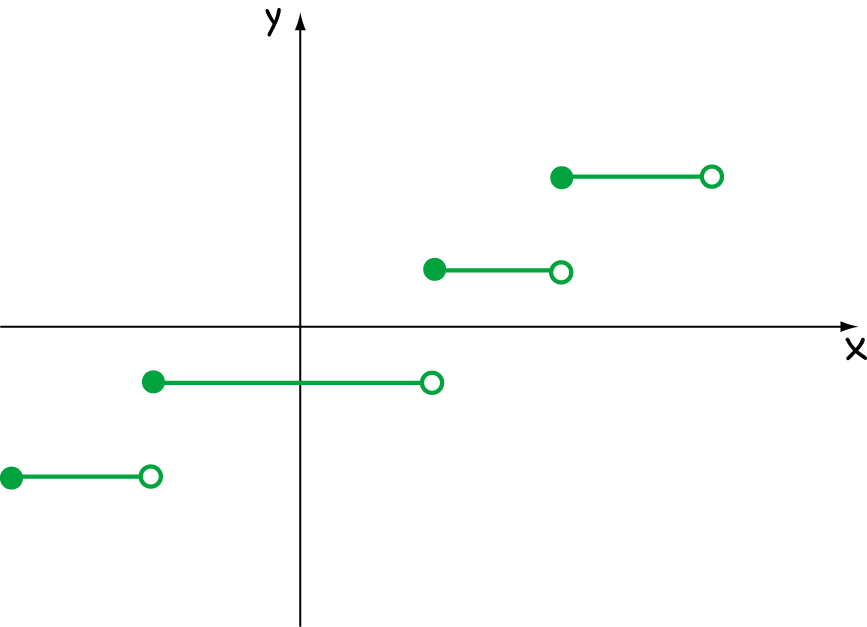
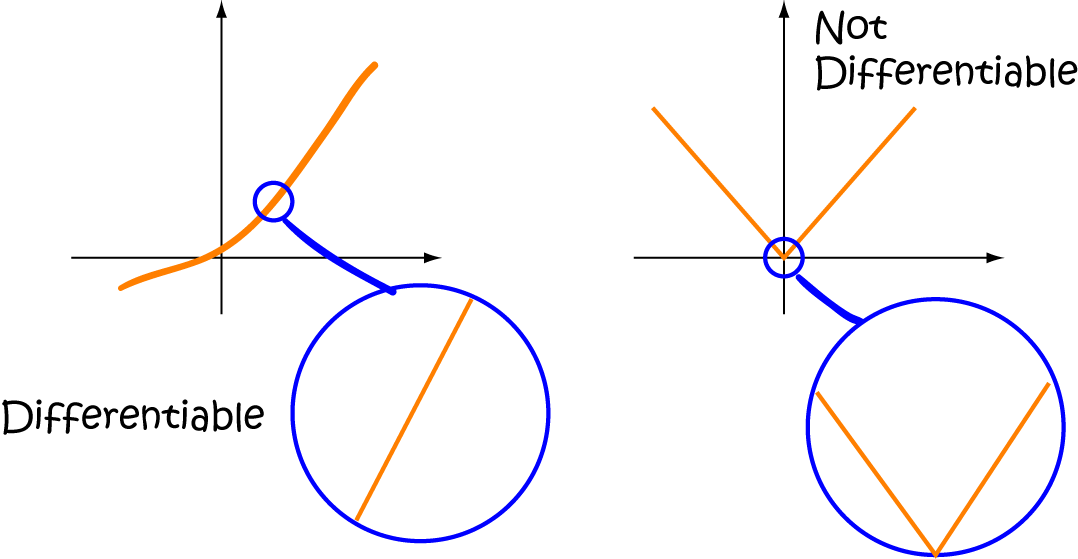
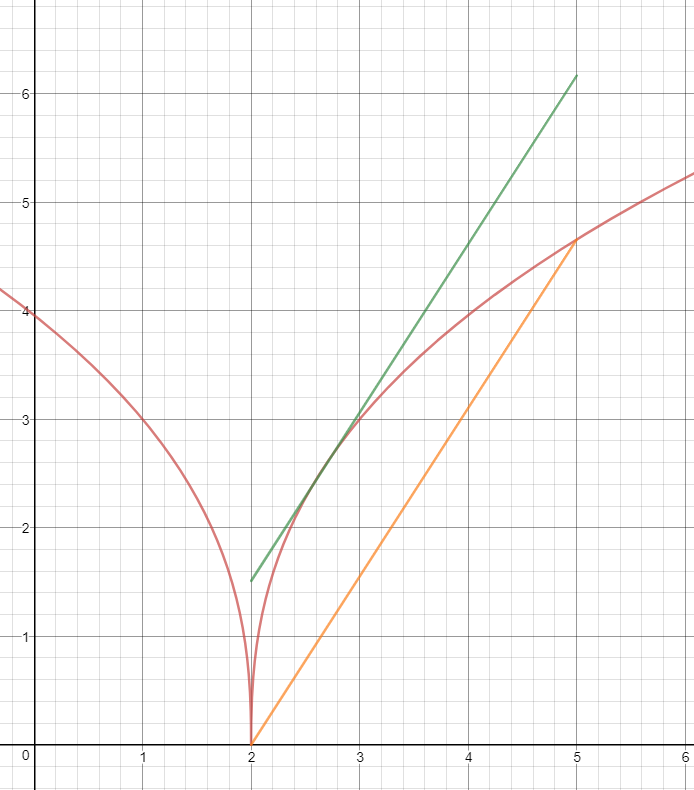
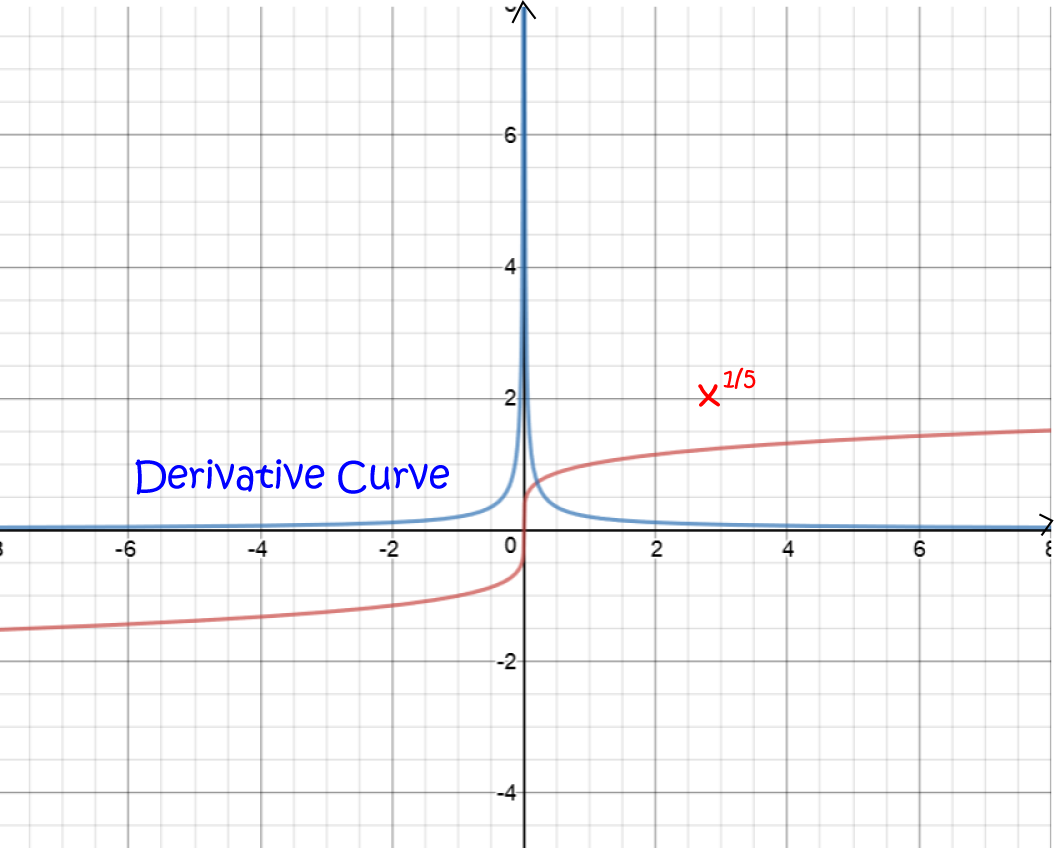
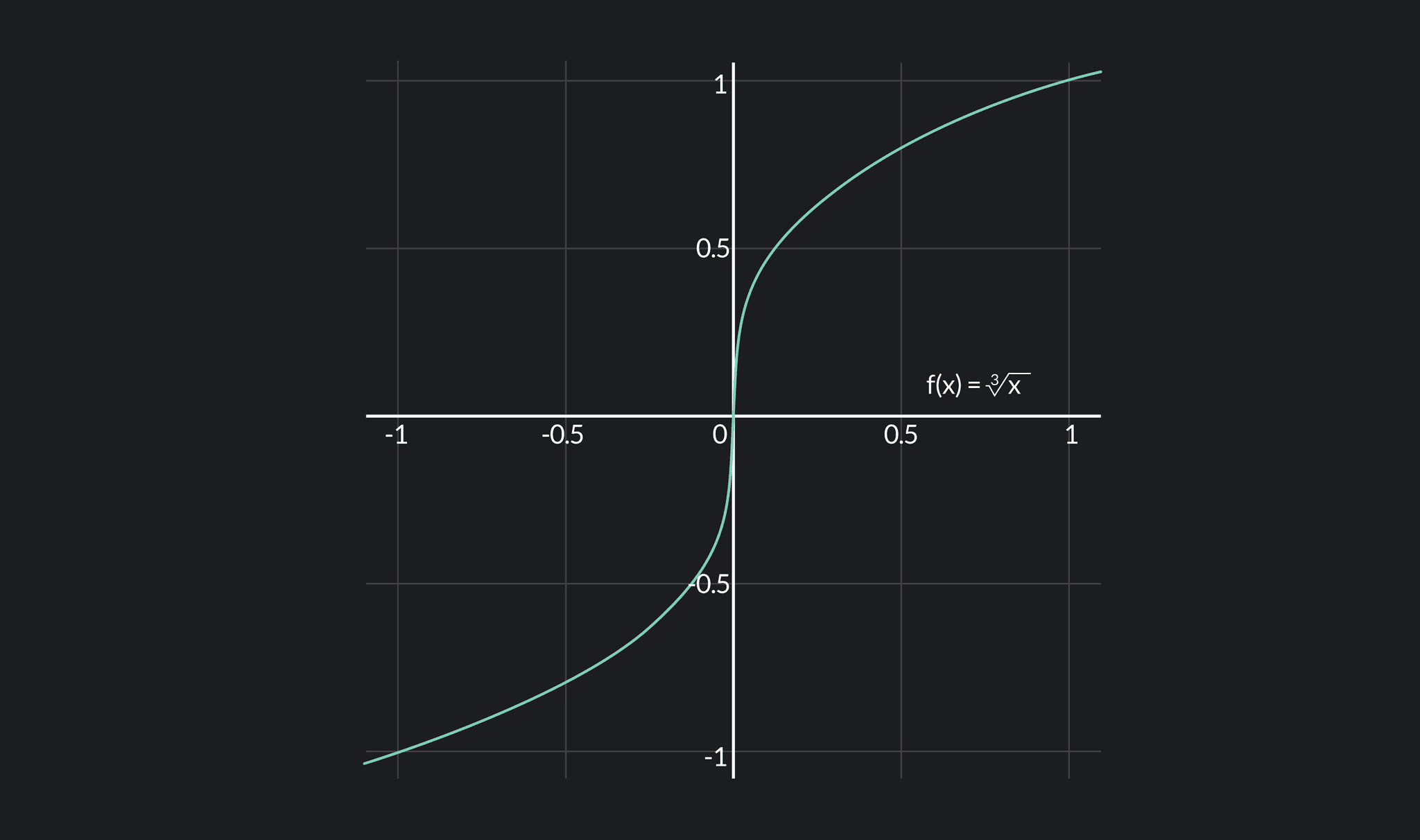What Does It Mean If A Function Is Differentiable - A function is differentiable (has a derivative) at point x if the following limit exists: A function which is differentiable everywhere will exhibit this sort of consistent. By definition, if x is a point in the domain of a function f, then f is said to be. So a point where the function is not differentiable is a point where this limit does not exist, that is,.
A function which is differentiable everywhere will exhibit this sort of consistent. By definition, if x is a point in the domain of a function f, then f is said to be. So a point where the function is not differentiable is a point where this limit does not exist, that is,. A function is differentiable (has a derivative) at point x if the following limit exists:
By definition, if x is a point in the domain of a function f, then f is said to be. So a point where the function is not differentiable is a point where this limit does not exist, that is,. A function which is differentiable everywhere will exhibit this sort of consistent. A function is differentiable (has a derivative) at point x if the following limit exists:
Differentiable function Wikiwand
By definition, if x is a point in the domain of a function f, then f is said to be. So a point where the function is not differentiable is a point where this limit does not exist, that is,. A function which is differentiable everywhere will exhibit this sort of consistent. A function is differentiable (has a derivative) at.
What does it mean for a function to be differentiable? Calculus
A function which is differentiable everywhere will exhibit this sort of consistent. By definition, if x is a point in the domain of a function f, then f is said to be. So a point where the function is not differentiable is a point where this limit does not exist, that is,. A function is differentiable (has a derivative) at.
Differentiable Function Meaning, Formulas and Examples Outlier
By definition, if x is a point in the domain of a function f, then f is said to be. A function is differentiable (has a derivative) at point x if the following limit exists: A function which is differentiable everywhere will exhibit this sort of consistent. So a point where the function is not differentiable is a point where.
What does it mean for a function to be differentiable? Calculus
A function is differentiable (has a derivative) at point x if the following limit exists: By definition, if x is a point in the domain of a function f, then f is said to be. So a point where the function is not differentiable is a point where this limit does not exist, that is,. A function which is differentiable.
Differentiable Function Meaning, Formulas and Examples Outlier
By definition, if x is a point in the domain of a function f, then f is said to be. A function which is differentiable everywhere will exhibit this sort of consistent. A function is differentiable (has a derivative) at point x if the following limit exists: So a point where the function is not differentiable is a point where.
What does it mean for a function to be differentiable? Calculus
By definition, if x is a point in the domain of a function f, then f is said to be. So a point where the function is not differentiable is a point where this limit does not exist, that is,. A function is differentiable (has a derivative) at point x if the following limit exists: A function which is differentiable.
Why is the function not differentiable? Socratic
A function is differentiable (has a derivative) at point x if the following limit exists: So a point where the function is not differentiable is a point where this limit does not exist, that is,. By definition, if x is a point in the domain of a function f, then f is said to be. A function which is differentiable.
What does it mean for a function to be differentiable? Calculus
A function is differentiable (has a derivative) at point x if the following limit exists: A function which is differentiable everywhere will exhibit this sort of consistent. So a point where the function is not differentiable is a point where this limit does not exist, that is,. By definition, if x is a point in the domain of a function.
What does it mean for a function to be differentiable? Calculus
A function is differentiable (has a derivative) at point x if the following limit exists: So a point where the function is not differentiable is a point where this limit does not exist, that is,. By definition, if x is a point in the domain of a function f, then f is said to be. A function which is differentiable.
Differentiable Function Meaning, Formulas and Examples Outlier
A function which is differentiable everywhere will exhibit this sort of consistent. So a point where the function is not differentiable is a point where this limit does not exist, that is,. A function is differentiable (has a derivative) at point x if the following limit exists: By definition, if x is a point in the domain of a function.
So A Point Where The Function Is Not Differentiable Is A Point Where This Limit Does Not Exist, That Is,.
By definition, if x is a point in the domain of a function f, then f is said to be. A function which is differentiable everywhere will exhibit this sort of consistent. A function is differentiable (has a derivative) at point x if the following limit exists: